21.【阅读材料】:
①在△ABC中,若∠C=90°,由“三角形内角和为180°”得∠A+∠B=180°-∠C=180°-90°=90°.
②在△ABC中,若∠A+∠B=90°,由“三角形内角和为180°”得∠C=180°-(∠A+∠B)=180°-90°=90°.
【解决问题】:
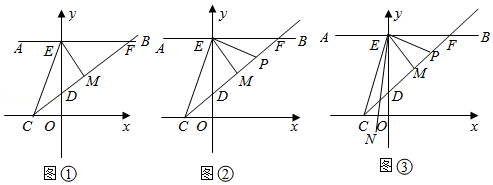
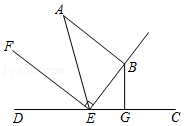
如图①,在平面直角坐标系中,点C是x轴负半轴上的一个动点.已知AB∥x轴,交y轴于点E,连接CE,CF是∠ECO的角平分线,交AB于点F,交y轴于点D.过E点作EM平分∠CEB,交CF于点M.
(1)试判断EM与CF的位置关系,并说明理由;
(2)如图②,过E点作PE⊥CE,交CF于点P,求证:∠EPC=∠EDP;
(3)在(2)的基础上,作EN平分∠AEP,交OC于点N,如图③.请问随着C点的运动,∠NEM的度数是否发生变化?若不变,求出其值;若变化,请说明理由.