21.国家创新指数是反映一个国家科学技术和创新竞争力的综合指数.对国家创新指数得分排名前40的国家的有关数据进行收集、整理、描述和分析.下面给出了部分信息:
A.国家创新指数得分的频数分布直方图(数据分成7组:30≤x<40,40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100);
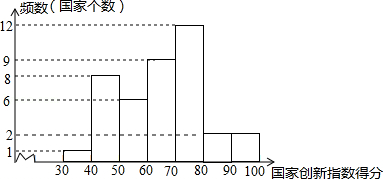
B.国家创新指数得分在60≤x<70这一组的是:
61.762.463.665.966.468.569.169.369.5
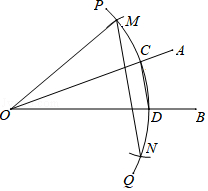
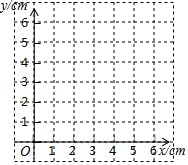
C.40个国家的人均国内生产总值和国家创新指数得分情况统计图:
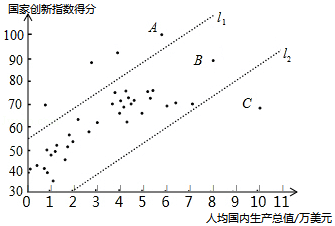
D.中国的国家创新指数得分为69.5.
(以上数据来源于《国家创新指数报告(2018)》)
根据以上信息,回答下列问题:
(1)中国的国家创新指数得分排名世界第
;
(2)在40个国家的人均国内生产总值和国家创新指数得分情况统计图中,包括中国在内的少数几个国家所对应的点位于虚线l
1的上方,请在图中用"〇"圈出代表中国的点;
(3)在国家创新指数得分比中国高的国家中,人均国内生产总值的最小值约为
万美元;(结果保留一位小数)
(4)下列推断合理的是
.
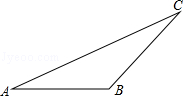
①相比于点A,B所代表的国家,中国的国家创新指数得分还有一定差距,中国提出"加快建设创新型国家"的战略任务,进一步提高国家综合创新能力;
②相比于点B,C所代表的国家,中国的人均国内生产总值还有一定差距,中国提出"决胜全面建成小康社会"的奋斗目标,进一步提高人均国内生产总值.