27.以下虚线框中为一个合作学习小组在一次数学实验中的过程记录,请阅读后完成虚线框下方的问题1~4.
(Ⅰ)在
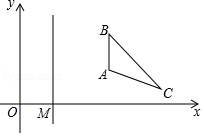
Rt△ABC中,∠C=90°,AB=2
√2
,在探究三边关系时,通过画图,度量和计算,收集到一组数据如下表:(单位:厘米)
| AC | 2.8 | 2.7 | 2.6 | 2.3 | 2 | 1.5 | 0.4 |
| BC | 0.4 | 0.8 | 1.2 | 1.6 | 2 | 2.4 | 2.8 |
| AC+BC | 3.2 | 3.5 | 3.8 | 3.9 | 4 | 3.9 | 3.2 |
(Ⅱ)根据学习函数的经验,选取上表中BC和AC+BC的数据进行分析:
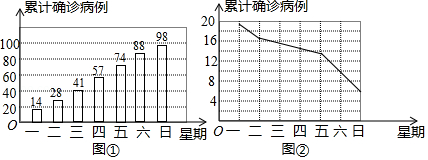
①BC=x,AC+BC=y,以(x,y)为坐标,在图①所示的坐标系中描出对应的点:
②连线:
观察思考
(Ⅲ)结合表中的数据以及所画的图象,猜想.当x=____时,y最大;
(Ⅳ)进一步猜想:若
Rt△ABC中,∠C=90°,斜边AB=2a(a为常数,a>0),则BC=____时,AC+BC最大.
推理证明
(Ⅴ)对(Ⅳ)中的猜想进行证明.
(1)问题1,在图①中完善(Ⅱ)的描点过程,并依次连线;
(2)问题2,补全观察思考中的两个猜想:(Ⅲ)
;(Ⅳ)
;
(3)问题3,证明上述(Ⅴ)中的猜想;
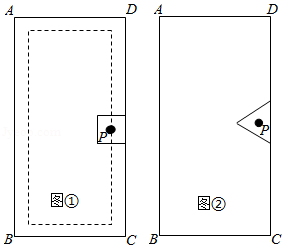
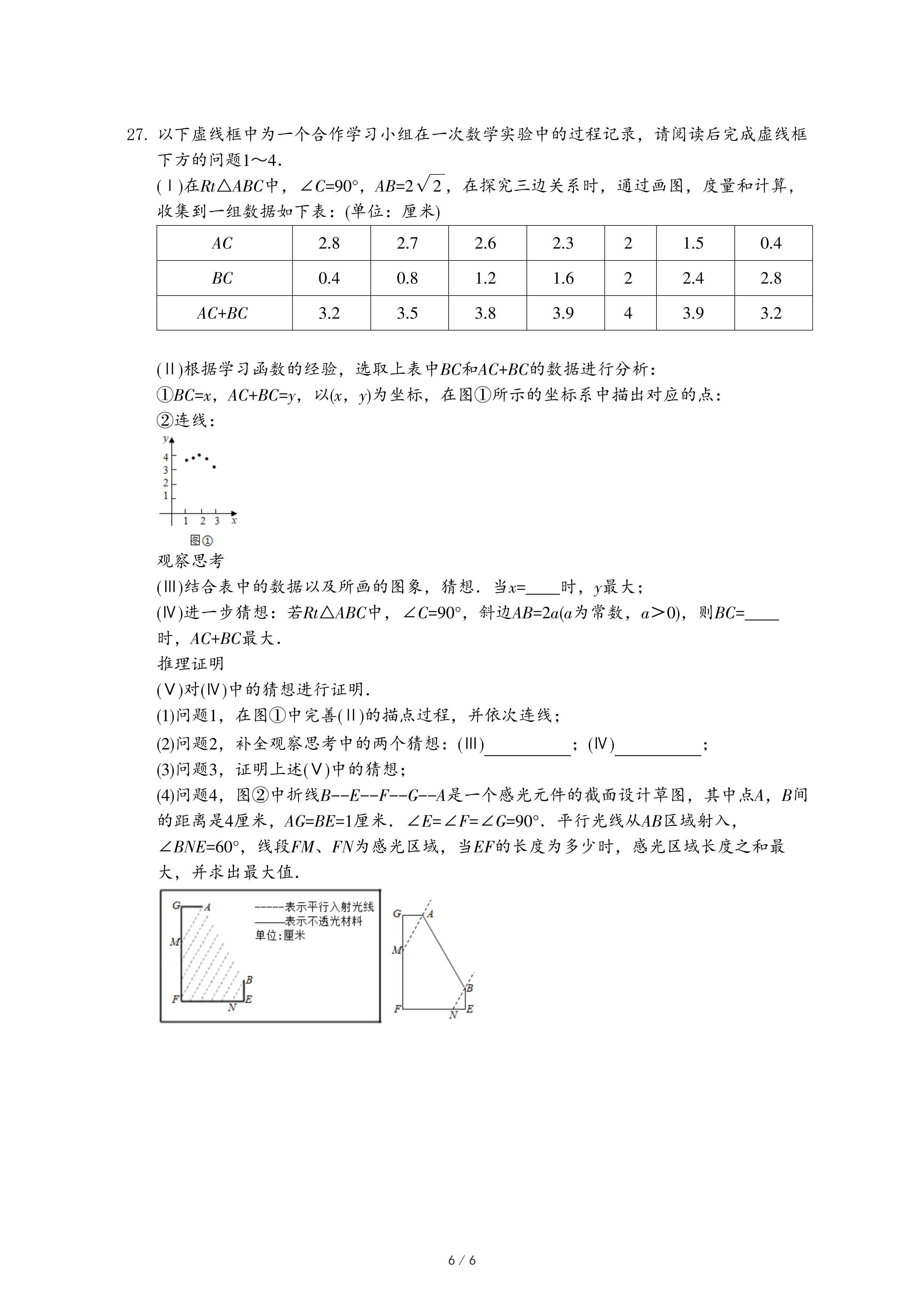
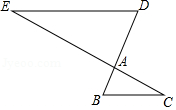
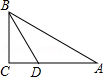
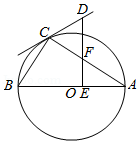
(4)问题4,图②中折线B--E--F--G--A是一个感光元件的截面设计草图,其中点A,B间的距离是4厘米,AG=BE=1厘米.∠E=∠F=∠G=90°.平行光线从AB区域射入,∠BNE=60°,线段FM、FN为感光区域,当EF的长度为多少时,感光区域长度之和最大,并求出最大值.











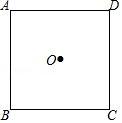

 厘米的等边三角形时,刻刀的位置仍在模具的中心点P处,雕刻时也始终保持模具的一边紧贴木门的一边,使模具进行滑动雕刻.但当模具的一个顶点与木门的一个顶点重合时,需将模具绕着重合点进行旋转雕刻,直到模具的另一边与木门的另一边重合.再滑动模具进行雕刻,如此雕刻一周,请在图②中画出雕刻所得图案的草图,并求其周长.
厘米的等边三角形时,刻刀的位置仍在模具的中心点P处,雕刻时也始终保持模具的一边紧贴木门的一边,使模具进行滑动雕刻.但当模具的一个顶点与木门的一个顶点重合时,需将模具绕着重合点进行旋转雕刻,直到模具的另一边与木门的另一边重合.再滑动模具进行雕刻,如此雕刻一周,请在图②中画出雕刻所得图案的草图,并求其周长.