19．计算：-(-1)²-(π-1)⁰+2^-1．

20．解方程组和不等式组：
(1)；
(2)．

21．为降低处理成本，减少土地资源消耗，我国正在积极推进垃圾分类政策，引导居民根据“厨余垃圾”、“有害垃圾”、“可回收物”和“其他垃圾”这四类标准将垃圾分类处理．调查小组就某小区居民对垃圾分类知识的了解程度进行了抽样调查，并根据调查结果绘制成统计图．
(1)本次调查的样本容量是       ；
(2)补全条形统计图；
(3)已知该小区有居民2000人，请估计该小区对垃圾分类知识“完全了解”的居民人数．

22．在3张相同的小纸条上，分别写上条件：①四边形ABCD是菱形；②四边形ABCD有一个内角是直角；③四边形ABCD的对角线相等．将这3张小纸条做成3支签，放在一个不透明的盒子中．
(1)搅匀后从中任意抽出1支签，抽到条件①的概率是       ；
(2)搅匀后先从中任意抽出1支签(不放回)，再从余下的2支签中任意抽出1支签．四边形ABCD同时满足抽到的2张小纸条上的条件，求四边形ABCD一定是正方形的概率．

23．如图，B、F、C、E是直线l上的四点，AB∥DE，AB=DE，BF=CE．
(1)求证：△ABC≌△DEF；
(2)将△ABC沿直线l翻折得到△A′BC．
①用直尺和圆规在图中作出△A′BC(保留作图痕迹，不要求写作法)；
②连接A′D，则直线A′D与l的位置关系是       ．

24．为落实节约用水的政策，某旅游景点进行设施改造，将手拧水龙头全部更换成感应水龙头．已知该景点在设施改造后，平均每天用水量是原来的一半，20吨水可以比原来多用5天．该景点在设施改造后平均每天用水多少吨？

25．如图，在平面直角坐标系xOy中，一次函数y=x+b的图象分别与x轴、y轴交于点A、B，与反比例函数y=(x＞0)的图象交于点C，连接OC．已知点A(-4，0)，AB=2BC．
(1)求b、k的值；
(2)求△AOC的面积．

26．【阅读】
通过构造恰当的图形，可以对线段长度、图形面积大小等进行比较，直观地得到一些不等关系或最值，这是“数形结合”思想的典型应用．
【理解】
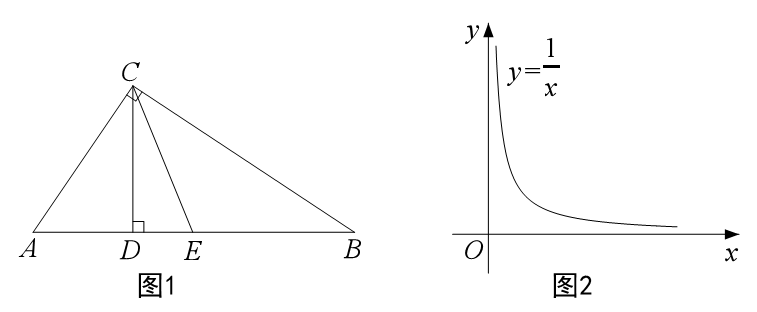
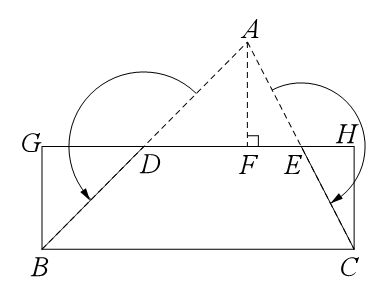
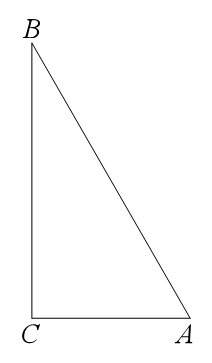
(1)如图1，AC⊥BC，CD⊥AB，垂足分别为C、D，E是AB的中点，连接CE．已知AD=a，BD=b(0＜a＜b)．
①分别求线段CE、CD的长(用含a、b的代数式表示)；
②比较大小：CE       CD(填“＜”、“=”或“＞”)，并用含a、b的代数式表示该大小关系．
【应用】
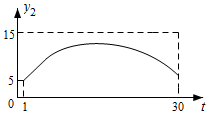
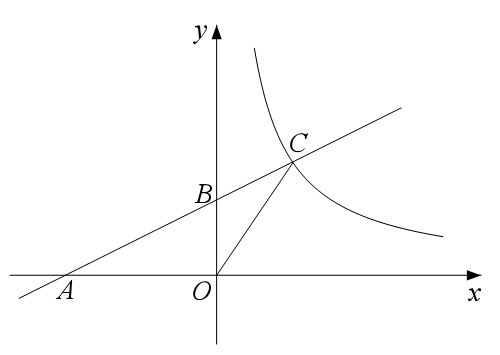
(2)如图2，在平面直角坐标系xOy中，点M、N在反比例函数y=(x＞0)的图象上，横坐标分别为m、n．设p=m+n，q=+，记l=pq．
①当m=1，n=2时，l=    ；当m=3，n=3时，l=      ；
②通过归纳猜想，可得l的最小值是       ．请利用图2构造恰当的图形，并说明你的猜想成立．

27．在平面直角坐标系xOy中，对于A、A′两点，若在y轴上存在点T，使得∠ATA′=90°，且TA=TA′，则称A、A′两点互相关联，把其中一个点叫做另一个点的关联点．已知点M(-2，0)、N(-1，0)，点Q(m，n)在一次函数y=-2x+1的图象上．
(1)①如图，在点B(2，0)、C(0，-1)、D(-2，-2)中，点M的关联点是       (填“B”、“C”或“D”)；
②若在线段MN上存在点P(1，1)的关联点P′，则点P′的坐标是       ；
(2)若在线段MN上存在点Q的关联点Q′，求实数m的取值范围；
(3)分别以点E(4，2)、Q为圆心，1为半径作⊙E、⊙Q．若对⊙E上的任意一点G，在⊙Q上总存在点G′，使得G、G′两点互相关联，请直接写出点Q的坐标．

28．如图，在平面直角坐标系xOy中，正比例函数y=kx(k≠0)和二次函数y=-x²+bx+3的图象都经过点A(4，3)和点B，过点A作OA的垂线交x轴于点C．D是线段AB上一点(点D与点A、O、B不重合)，E是射线AC上一点，且AE=OD，连接DE，过点D作x轴的垂线交抛物线于点F，以DE、DF为邻边作▱DEGF．
(1)填空：k=      ，b=      ；
(2)设点D的横坐标是t(t＞0)，连接EF．若∠FGE=∠DFE，求t的值；
(3)过点F作AB的垂线交线段DE于点P若S_△DFP=S_▱DEGF，求OD的长．