27.在学习利用旋转解决图形问题时,老师提出如下问题:
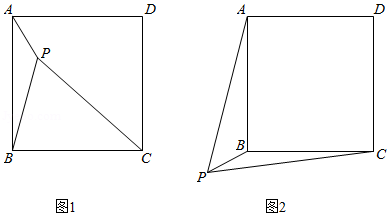
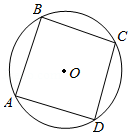
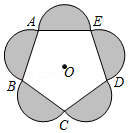
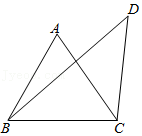
(1)如图1,点P是正方形ABCD内一点,PA=1,PB=2,PC=3,你能求出∠APB的度数吗?
小明通过观察、分析、思考,形成了如下思路:
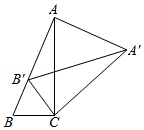
思路一:将△PBC绕点B逆时针旋转90°,得到△P'BA,连接PP',可求出∠APB的度数;
思路二:将△PAB绕点B顺时针旋转90°,得到△P'CB,连接PP',可求出∠APB的度数;
请参照小明的思路,任选一种写出完整的解答过程;
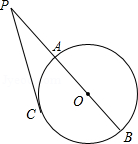
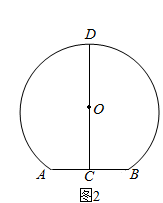
(2)如图2,若点P是正方形ABCD外一点,要使∠APB=45°,线段PA,PB,PC应满足怎样的等量关系?
请参考小明上述解决问题的方法进行探究,直接写出线段PA,PB,PC满足的等量关系.