19．计算：
(1)+-；
(2)(2+)(2-)．

20．已知一次函数的图象经过点(-2，-2)，(2，4)．
(1)求该一次函数的解析式；
(2)在坐标系中画出该一次函数的图象，观察图象，直接写出当x≥0时，y的取值范围．

21．学习完四边形的知识后，小明想出了“作三角形一边中线”的另一种尺规作图的作法，下面是具体过程．
已知：△ABC．
求作：BC边上的中线AD．
作法：如图，
①分别以点B，C为圆心，AC，AB长为半径作弧，两弧相交于P点；
②作直线AP，AP与BC交于D点，所以线段AD就是所求作的中线．
根据小明设计的尺规作图过程，
(1)使用直尺和圆规，补全图形；(保留作图痕迹)
(2)完成下面的证明．
证明：连接PB，PC．
∵PC=AB，      ，
∴四边形ABPC是平行四边形(      )(填推理的依据)．
∴DB=DC(      )(填推理的依据)．
∴AD是BC边上的中线．

22．在平面直角坐标系xOy中，直线l₁：y=2x与直线l₂：y=-x+3相交于点A，直线l₂与x轴交于点B．
(1)求△OAB的面积；
(2)过动点P(0，n)作垂直于y轴的直线与l₁，l₂的交点分别为C(x₁，y₁)，D(x₂，y₂)，当|x₁-x₂|≥3时，直接写出n的取值范围．

23．如图，在Rt△ABC中，∠ABC=90°，D、E分别是边BC，AC的中点，连接ED并延长到点F，使DF=ED，连接BE、BF、CF、AD．
(1)求证：四边形BFCE是菱形；
(2)若BC=4，EF=2，求AD的长．

24．现代互联网技术的广泛应用，催生了快递行业的高速发展，小明计划给朋友快递一部分物品，经了解甲、乙两家快递公司比较合适，
甲公司表示：快递物品不超过1千克的，收费12元；超过1千克，超过的部分按单价每千克2元收费．
乙公司表示：快递物品不超过1千克的，收费10元；超过1千克，超过的部分按单价每千克4元收费．
例如：小明要快递1.4千克的物品，选甲公司需付费12.8元，选乙公司需付费11.6元．
设小明快递物品x千克．
(1)请分别直接写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式；
(2)如果只考虑价格，不考虑其它因素，小明选择哪家快递公司更省钱？

25．在平面直角坐标系xOy中，已知点A(-3，1)，B(-1，1)，C(m，3)，以点A，B，C为顶点的平行四边形有三个，记第四个顶点分别为D₁，D₂，D₃，如图所示．
(1)若m=-1，则点D₁，D₂，D₃的坐标分别是 (      )，(      )，(      )；
(2)若△D₁D₂D₃是以D₁D₂为底的等腰三角形，
①直接写出m的值；
②若直线y=x+b与△D₁D₂D₃有公共点，求b的取值范围．
(3)若直线y=x与△D₁D₂D₃有公共点，求m的取值范围．

26．已知正方形ABCD，点E，F分别在射线BC，射线CD上，BE=CF，AE与BF交于点H．
(1)如图1，当点E，F分别在线段BC，CD上时，求证：AE=BF，且AE⊥BF；
(2)如图2，当点E在线段BC延长线上时，将线段BE沿BF平移至FG，连接AG．
①依题意将图2补全；
②用等式表示线段AG，FG和AD之间的数量关系，并证明．

27．在平面直角坐标系xOy中，对于图形M，N给出如下定义：P为图形M上任意一点，Q为图形N上任意一点，如果P，Q两点间的距离有最大值，那么称这个最大值为图形M和N的“极大距离”，记为d(M，N)．
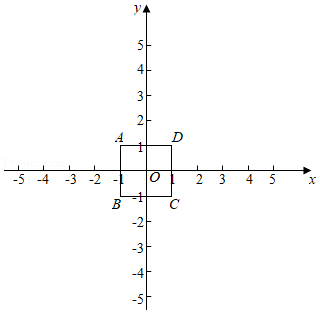
已知：正方形ABCD，其中A(-1，1)，B(-1，-1)，C(1，-1)，D(1，1)．
(1)已知点P(0，t)，
①若t=3，则d(点P，正方形ABCD)=      ；
②若d(点P，正方形ABCD)=3，则t=      ．
(2)已知点E(m，3)，F(m+2，3)，若5＜d(线段EF，正方形ABCD)＜2，求m的取值范围．
(3)一次函数y=kx+3的图象与x轴交于点G，与y轴交于点H，求d(线段GH，正方形ABCD)的最小值，并直接写出此时k的取值范围．