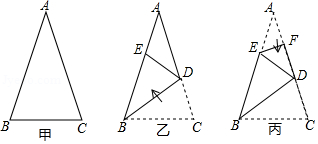
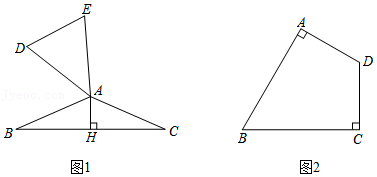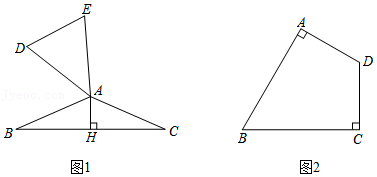28.若△ABC和△ADE均为等腰三角形,且AB=AC=AD=AE,当∠ABC和∠ADE互余时,称△ABC与△ADE互为“底余等腰三角形”, △ABC的边BC上的高AH叫做△ADE的“余高”.
(1)如图1,△ABC与△ADE互为“底余等腰三角形”.
①若连接BD,CE,判断△ABD与△ACE是否互为“底余等腰三角形”:
(填“是”或“否” );
②当∠BAC=90°时,若△ADE的“余高” AH=
√5
,则DE=
.
③当0°<∠BAC<180°时,判断DE与AH之间的数量关系,并证明;
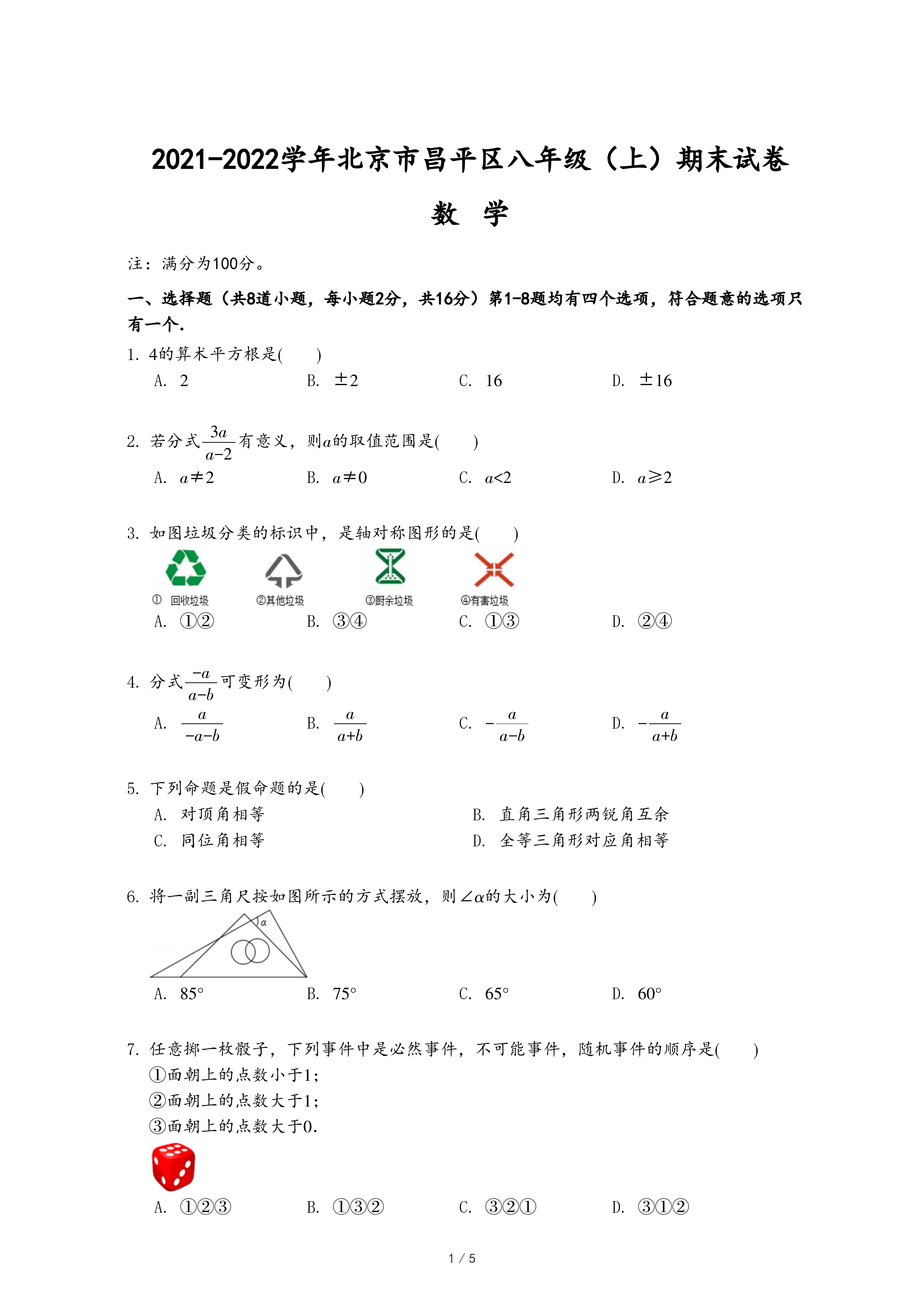
(2)如图2,在四边形ABCD中,∠ABC=60°,DA⊥BA,DC⊥BC,且DA=DC.
①画出△OAB与△OCD,使它们互为“底余等腰三角形”;
②若△OCD的“余高”长为a,则点A到BC的距离为
.(用含a的式子表示)