



√3 |
| 3 |
| 1 |
| 3 |
| 22 |
| 7 |
| 行列 | 第1列 | 第2列 | 第3列 | 第4列 |
| 第1行 | 1 | √2 | √3 | 2 |
| 第2行 | 2 √2 | √7 | √6 | √5 |
| 第3行 | 3 | √10 | √11 | 2 √3 |
| 第4行 | 4 | √15 | √14 | √13 |
| … | … | … | … | … |
| 4 |
| 5 |
| 1 |
| 9 |
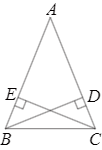
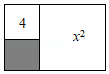
| 例题:说明代数式m2+2m+4的值一定是正数.解:m2+2m+4=m2+2m+1+3=(m+1)2+3,∵(m+1)2≥0,∴(m+1)2+3≥3,∴m2+2m+4的值一定是正数. |
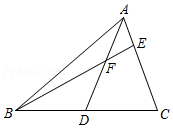
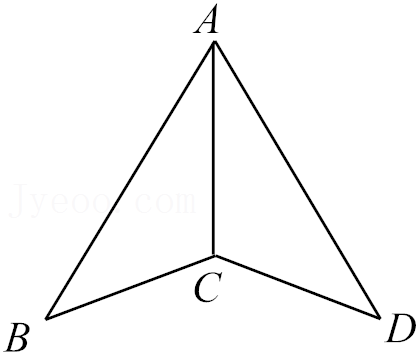
思路一:如图①,添加辅助线后依据SAS可证得△ADC≌△GDB,再利用AE=EF可以进一步证得∠G=∠FAE=∠AFE=∠BFG,从而证明结论.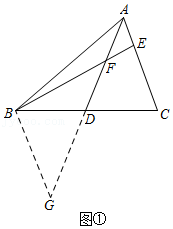 |
思路二:如图②,添加辅助线后并利用AE=EF可证得∠G=∠BFG=∠AFE=∠FAE,再依据AAS可以进一步证得△ADC≌△GDB,从而证明结论.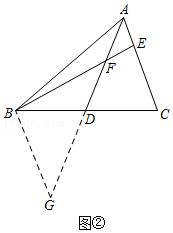 |
| “友好数对”已知两个两位数,将它们各自的十位数字和个位数字交换位置后,得到两个与原两个两位数均不同的新数,若这两个两位数的乘积与交换位置后两个新两位数的乘积相等,则称这样的两个两位数为“友好数对”.例如43×68=34×86=2924,所以43和68与34和86都是“友好数对”. |