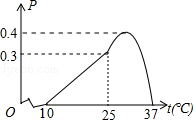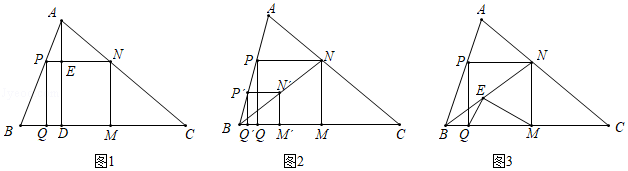



| 1 |
| 2019 |
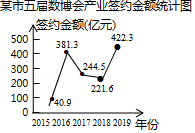
| 1 |
| 2019 |



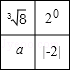
| a |
| c |
| b |
| c |
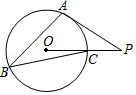
| 1 |
| 2 |
| { | 4x+6y=38 3x+5y=48 |
| { | 4y+6x=48 3y+5x=38 |
| { | 4x+6y=48 5x+3y=38 |
| { | 4x+6y=48 3x+5y=38 |
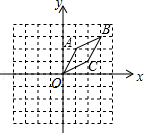
√5 |
| 5 |

| 1 |
| x+1 |
| 2 |
| x2-1 |
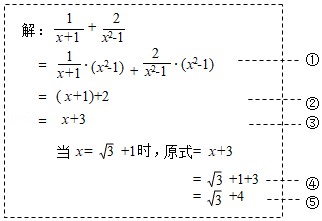
| k |
| x |
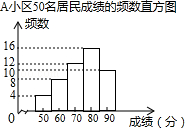
| 75 | 75 | 79 | 79 | 79 | 79 | 80 | 80 |
| 81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
| 小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
| A | 75.1 | 79 | 40% | 277 | |
| B | 75.1 | 77 | 76 | 45% | 211 |
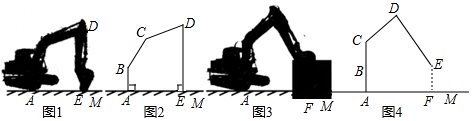
| 1 |
| 50 |
| 1 |
| 5 |
| 1 |
| 160 |
| 生长率p | 0.2 | 0.25 | 0.3 | 0.35 |
| 提前上市的天数m(天) | 0 | 5 | 10 | 15 |