










| 10 |
| 3 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
| 6 |
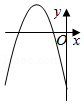
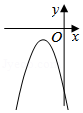
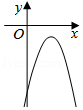
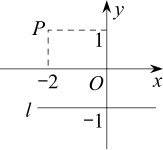
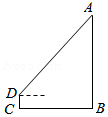
| 12 |
| x |
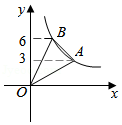
| 1 |
| 3 |
| 2x-1 |
| x-1 |
| x-2 |
| x2-2x+1 |
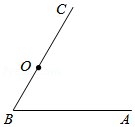
| 等级 | 成绩/分 | 频数 |
| A | 95≤x≤100 | a |
| B | 90≤x<95 | 8 |
| C | 85≤x<90 | 5 |
| D | 80≤x<85 | 4 |
| 原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
| 餐桌 | a | 380 | 940 |
| 餐椅 | a-140 | 160 |
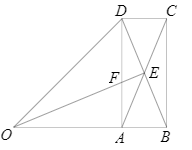
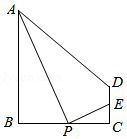
| BP/cm | … | 1 | 2 | 3 | 4 | 5 | … |
| CE/cm | … | 0.83 | 1.33 | 1.50 | 1.33 | 0.83 | … |
| BP/cm | … | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| CE/cm | … | 1.17 | 2.00 | 2.50 | 2.67 | 2.50 | 2.00 | 1.17 | … |
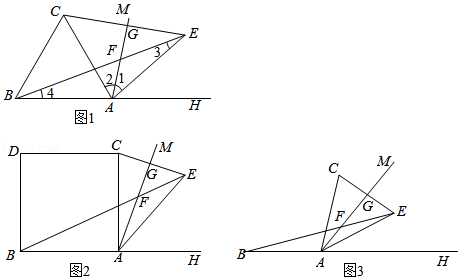
| 1 |
| 2 |
| 1 |
| 2 |