17．计算：x(x+2)+(1+x)(1-x)．

18．解分式方程：=1．

19．如图，已知经过原点的抛物线y=2x²+mx与x轴交于另一点A(2，0)．
(1)求m的值和抛物线顶点M的坐标；
(2)求直线AM的解析式．

20．为了更好地了解党的历史，宣传党的知识，传颂英雄事迹，某校团支部组建了：A．党史宣讲；B．歌曲演唱；C．校刊编撰；D．诗歌创作等四个小组，团支部将各组人数情况制成了统计图表(不完整)．
各组参加人数情况统计表

根据统计图表中的信息，解答下列问题：
(1)求a和m的值；
(2)求扇形统计图中D所对应的圆心角度数；
(3)若在某一周各小组平均每人参与活动的时间如下表所示：

求这一周四个小组所有成员平均每人参与活动的时间．

21．如图，已知AB是⊙O的直径，∠ACD是⌒AD所对的圆周角，∠ACD=30°．
(1)求∠DAB的度数；
(2)过点D作DE⊥AB，垂足为E，DE的延长线交⊙O于点F．若AB=4，求DF的长．

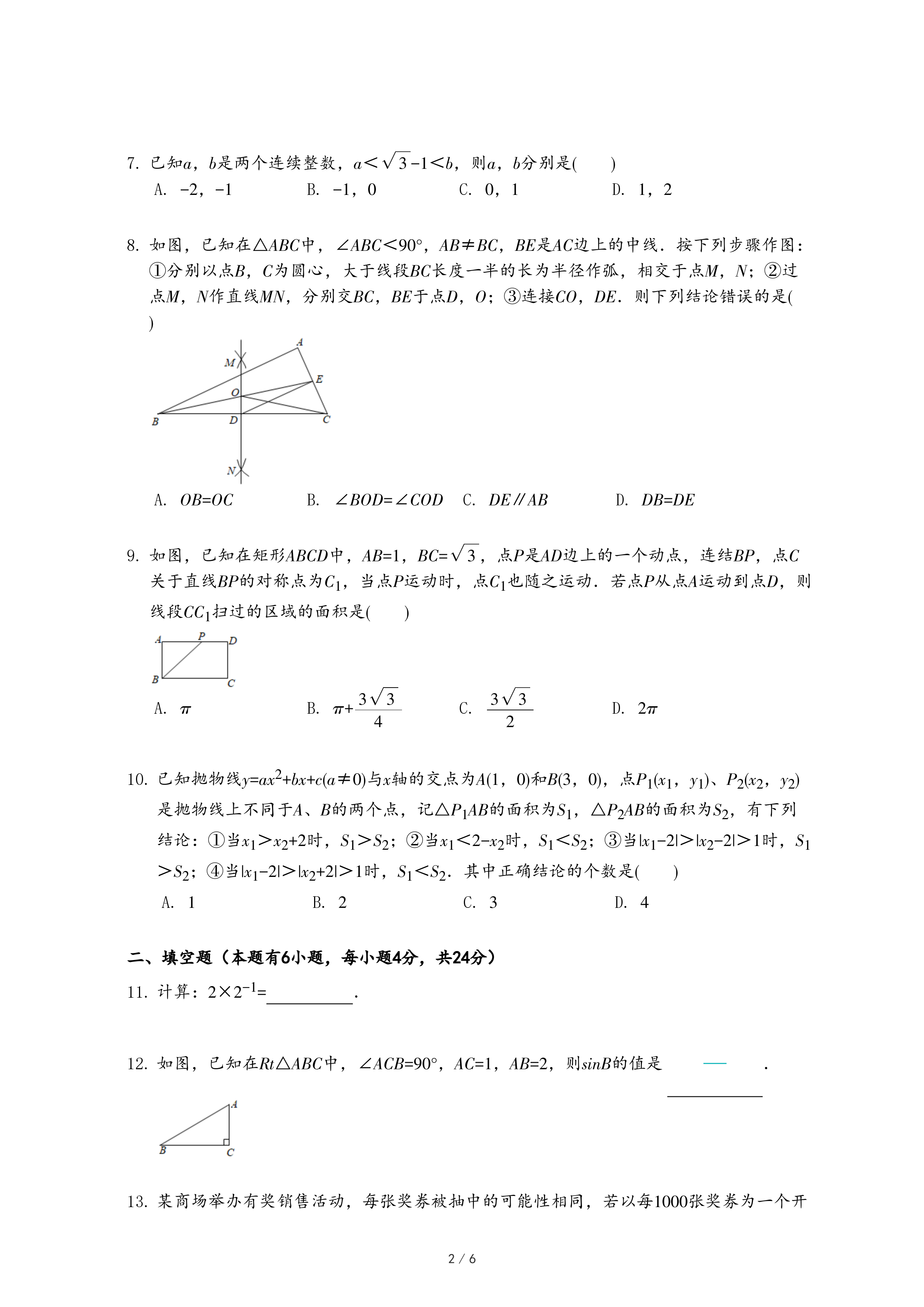
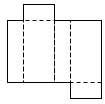
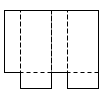
22．今年以来，我市接待的游客人数逐月增加，据统计，游玩某景区的游客人数三月份为4万人，五月份为5.76万人．
(1)求四月和五月这两个月中该景区游客人数平均每月增长百分之几；
(2)若该景区仅有A，B两个景点，售票处出示的三种购票方式如下表所示：

据预测，六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万，并且当甲、乙两种门票价格不变时，丙种门票价格每下降1元，将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票．
①若丙种门票价格下降10元，求景区六月份的门票总收入；
②问：将丙种门票价格下降多少元时，景区六月份的门票总收入有最大值？最大值是多少万元？

23．已知在△ACD中，P是CD的中点，B是AD延长线上的一点，连结BC，AP．

(1)如图1，若∠ACB=90°，∠CAD=60°，BD=AC，AP=，求BC的长．
(2)过点D作DE∥AC，交AP延长线于点E，如图2所示，若∠CAD=60°，BD=AC，求证：BC=2AP．
(3)如图3，若∠CAD=45°，是否存在实数m，当BD=mAC时，BC=2AP？若存在，请直接写出m的值；若不存在，请说明理由．

24．已知在平面直角坐标系xOy中，点A是反比例函数y=(x＞0)图象上的一个动点，连结AO，AO的延长线交反比例函数y=(k＞0，x＜0)的图象于点B，过点A作AE⊥y轴于点E．

(1)如图1，过点B作BF⊥x轴，于点F，连接EF．
①若k=1，求证：四边形AEFO是平行四边形；
②连结BE，若k=4，求△BOE的面积．
(2)如图2，过点E作EP∥AB，交反比例函数y=(k＞0，x＜0)的图象于点P，连结OP．试探究：对于确定的实数k，动点A在运动过程中，△POE的面积是否会发生变化？请说明理由．