28.对于△ABC及其边上的点P,给出如下定义:如果点M
1,M
2,M
3,……,M
n都在△ABC的边上,且PM
1=PM
2=PM
3=……=PM
n,那么称点M
1,M
2,M
3,……,M
n为△ABC关于点P的等距点,线段PM
1,PM
2,PM
3,……,PM
n为△ABC关于点P的等距线段.
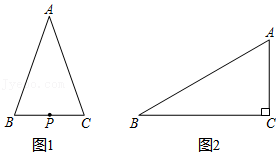
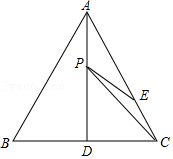
(1)如图1,△ABC中,∠A<90°,AB=AC,点P是BC的中点.
①点B,C
△ABC关于点P的等距点,线段PA,PB
△ABC关于点P的等距线段;(填“是”或“不是”)
②△ABC关于点P的两个等距点M
1,M
2分别在边AB,AC上,当相应的等距线段最短时,在图1中画出线段PM
1,PM
2;
(2)△ABC是边长为4的等边三角形,点P在BC上,点C,D是△ABC关于点P的等距点,且PC=1,求线段DC的长;
(3)如图2,在
Rt△ABC中,∠C=90°,∠B=30°.点P在BC上,△ABC关于点P的等距点恰好有四个,且其中一个是点C.若BC=a,直接写出PC长的取值范围.(用含a的式子表示)