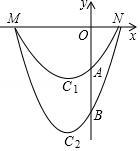
23.定义:由两条与x轴有着相同的交点,并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”.如图,抛物线C
1与抛物线C
2组成一个开口向上的“月牙线”,抛物线C
1与抛物线C
2与x轴有相同的交点M,N(点M在点N的左侧),与y轴的交点分别为A,B且点A的坐标为(0,-3),抛物线C
2的解析式为y=mx
2+4mx-12m,(m>0).
(1)请你根据“月牙线”的定义,设计一个开口向下的“月牙线”,直接写出两条抛物线的解析式;
(2)求M,N两点的坐标;
(3)在第三象限内的抛物线C
1上是否存在一点P,使得△PAM的面积最大?若存在,求出△PAM的面积的最大值;若不存在,说明理由.