22.阅读下列材料,完成相应的任务:
三角形数古希腊著名的毕达哥拉斯学派把1,3,6,10,…,这样的数称为“三角形数”,第n个“三角形数”可表示为:1+2+3+4+…+n=
;
任务:
(1)第5个三角形数是
;
(2)请从下面A,B两题中任选一题作答.我选择
题.
A.智慧小组发现,从第2个“三角形数”开始,每相邻两个“三角形数”的差有一定的规律.
如:3-1=2;6-3=3;10-6=4;…
①第6个“三角形数”与第5个“三角形数”的差为
;
②第n(n≥2)个“三角形数”与第(n-1)个“三角形数”的差的规律可用下面的等式表示
-
=n.请补全该等式并说明它的正确性.
B.创新小组发现,每相邻两个“三角形数”的和有一定的规律.
如:1+3=4;3+6=9;6+10=16;…
①第5个“三角形数”与第6个“三角形数”的和为
;
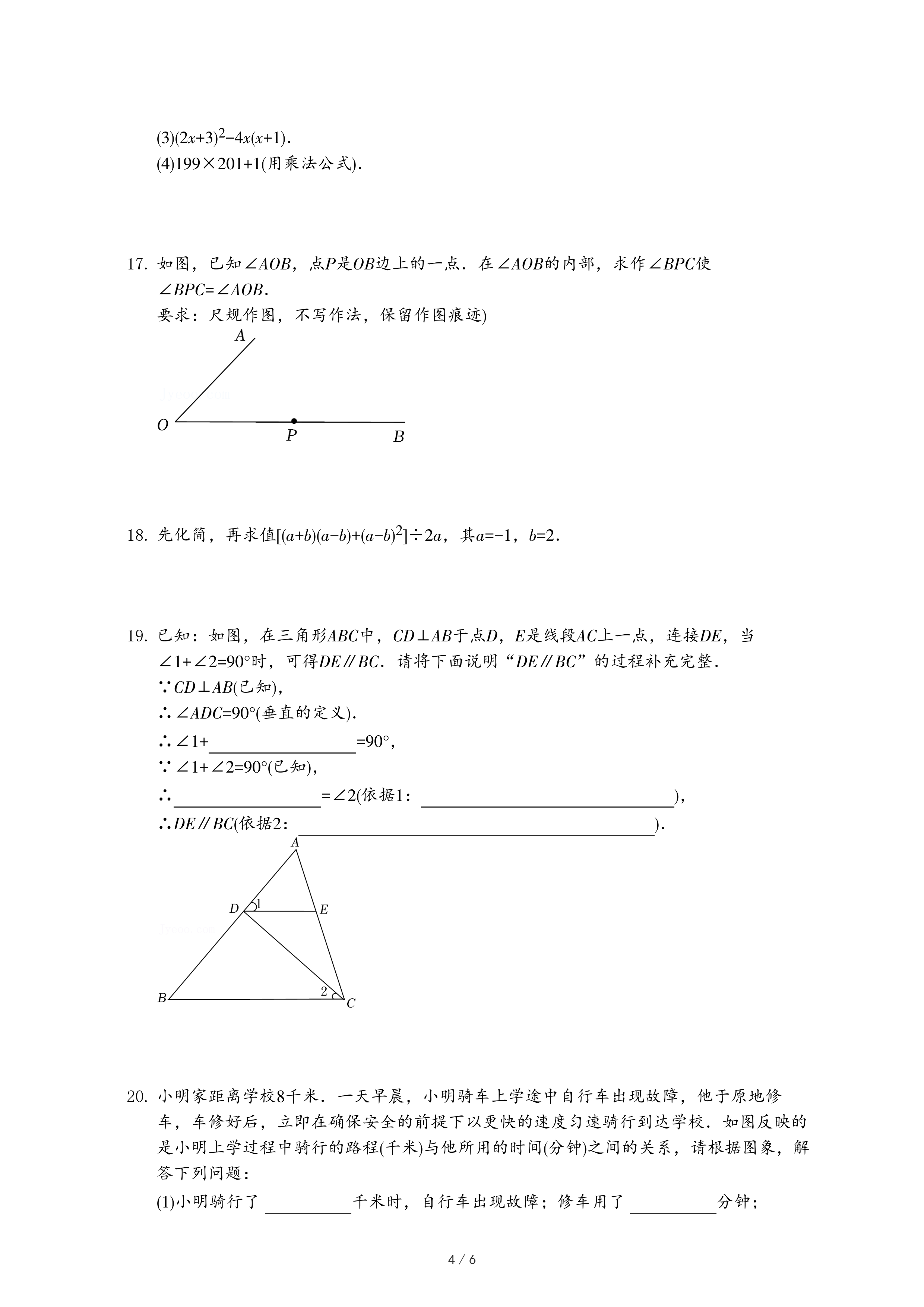
②第n个“三角形数”与第(n+1)个“三角形数”的和的规律可用下面的等式表示:
+
=
.请补全该等式并说明它的正确性.