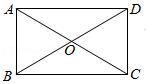
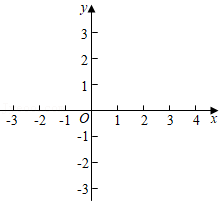26.阅读下列材料:
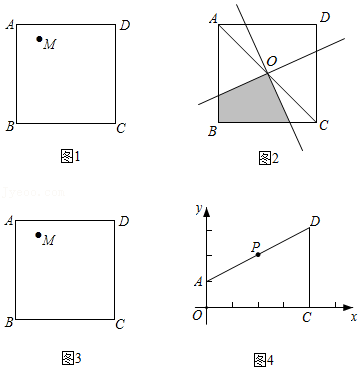
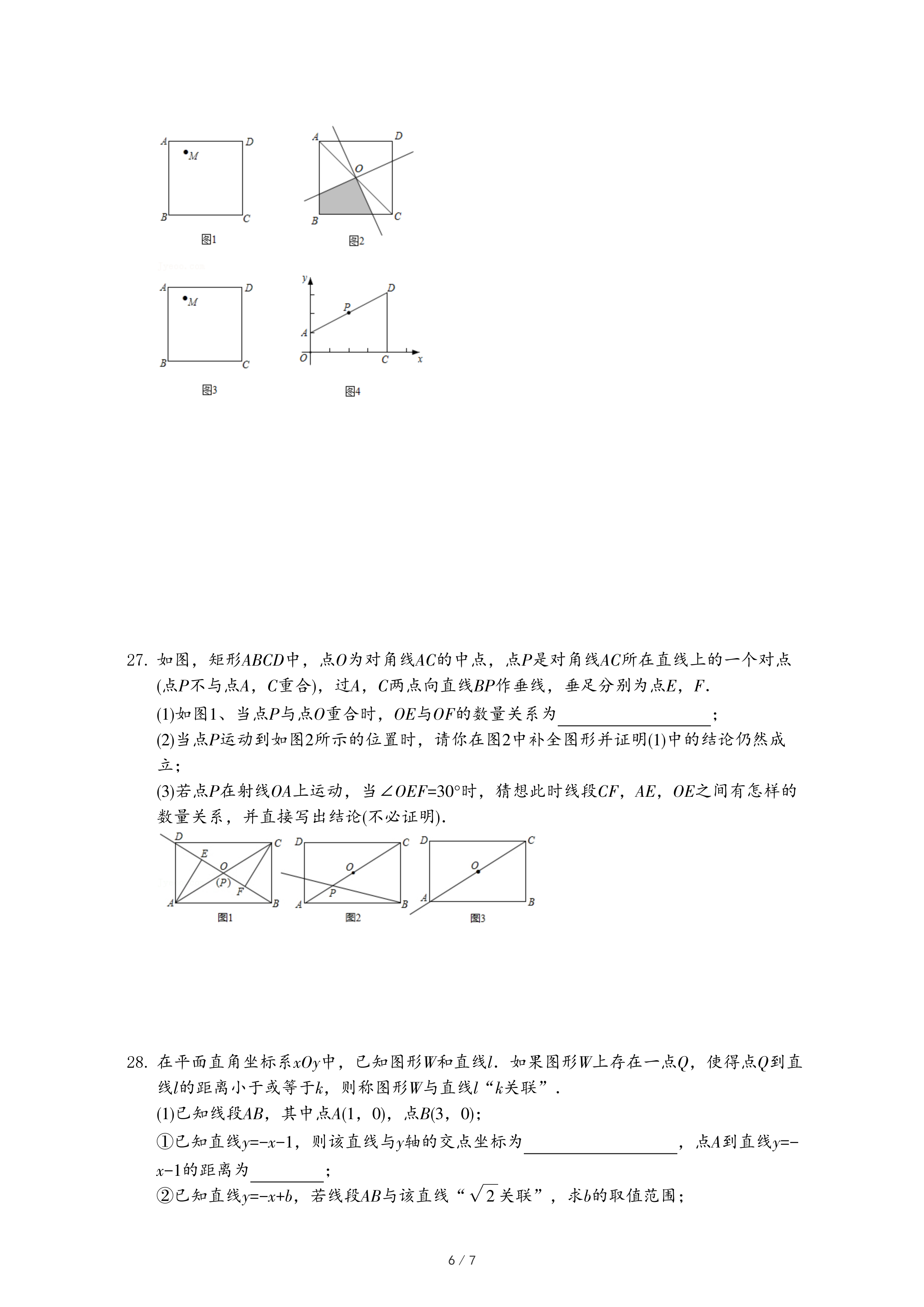
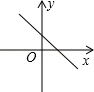
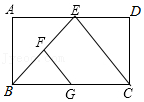
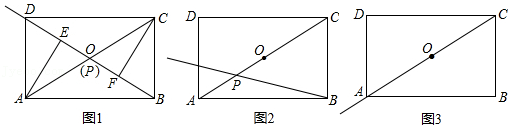
小明同学遇到了这样一个问题:如图1,M是边长为a的正方形ABCD内一定点,请在图中作出两条直线(要求其中一条直线必须过点M),将正方形ABCD的面积分割成面积相等的四个部分.
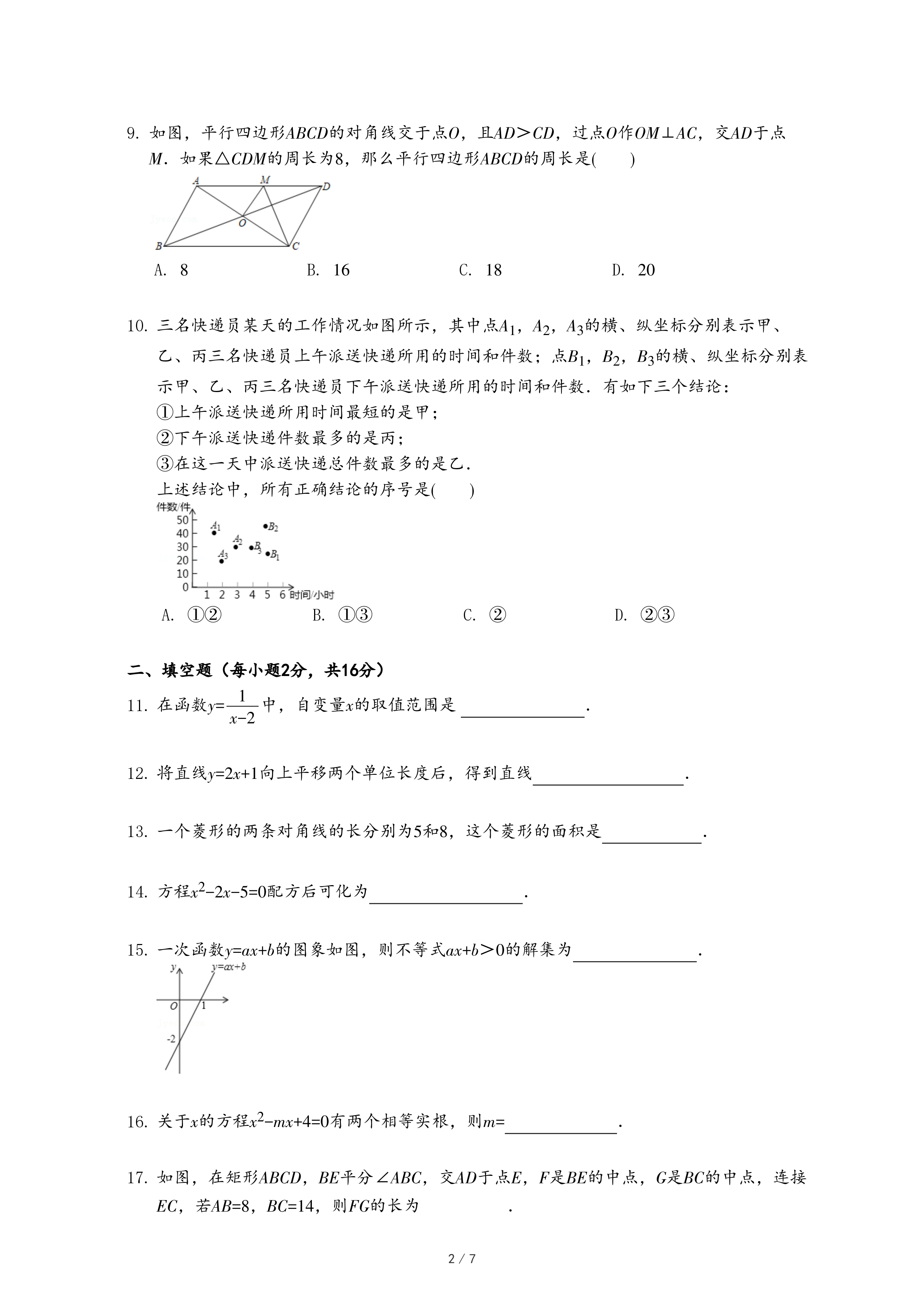
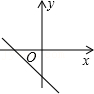
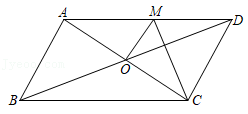
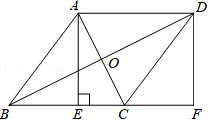
小明是这样思考的:数学课上曾经做过一道类似的题目,如图2,O是边长为a的正方形ABCD的对角线的交点,将以点O为顶点的直角绕点O旋转,且两直角边分别与BA,CB相交,与正方形重叠部分(即阴影部分)的面积为一个确定的值.可以类比解决此问题.
参考小明同学的想法,解答问题:
(1)请你回答图2中重叠部分(即阴影部分)的面积为
;
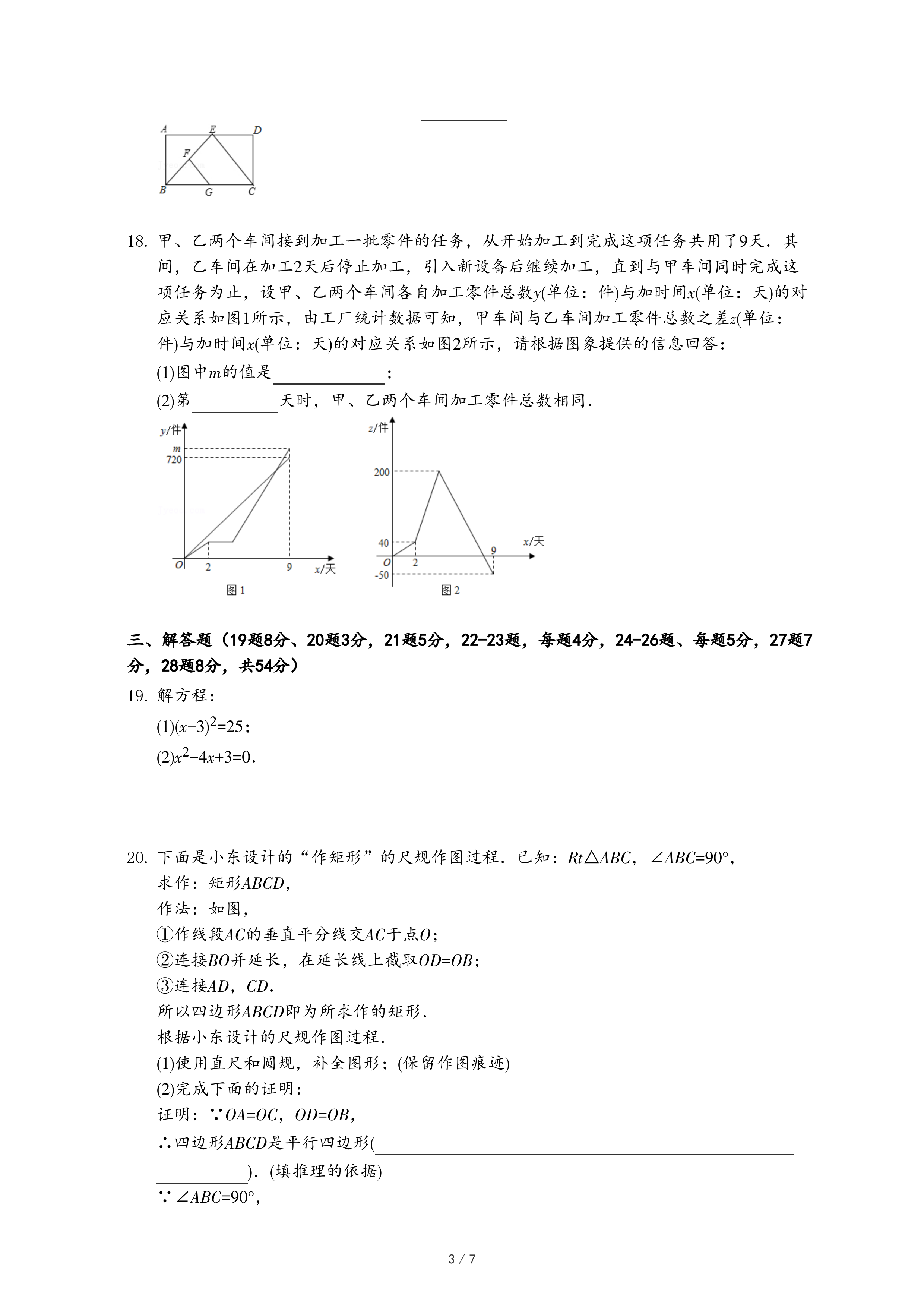
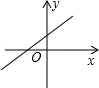
(2)请你在图3中,解决原问题:
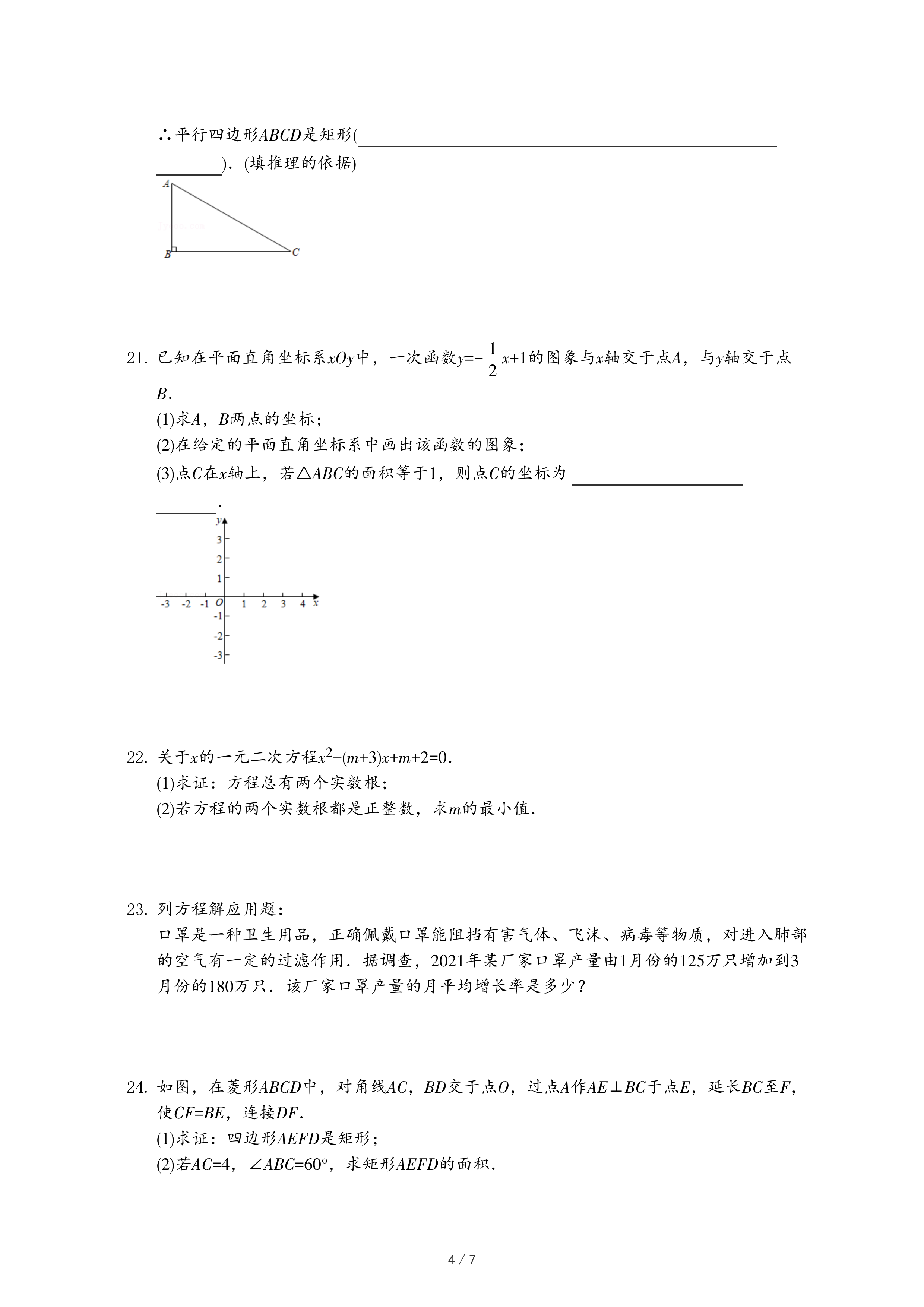
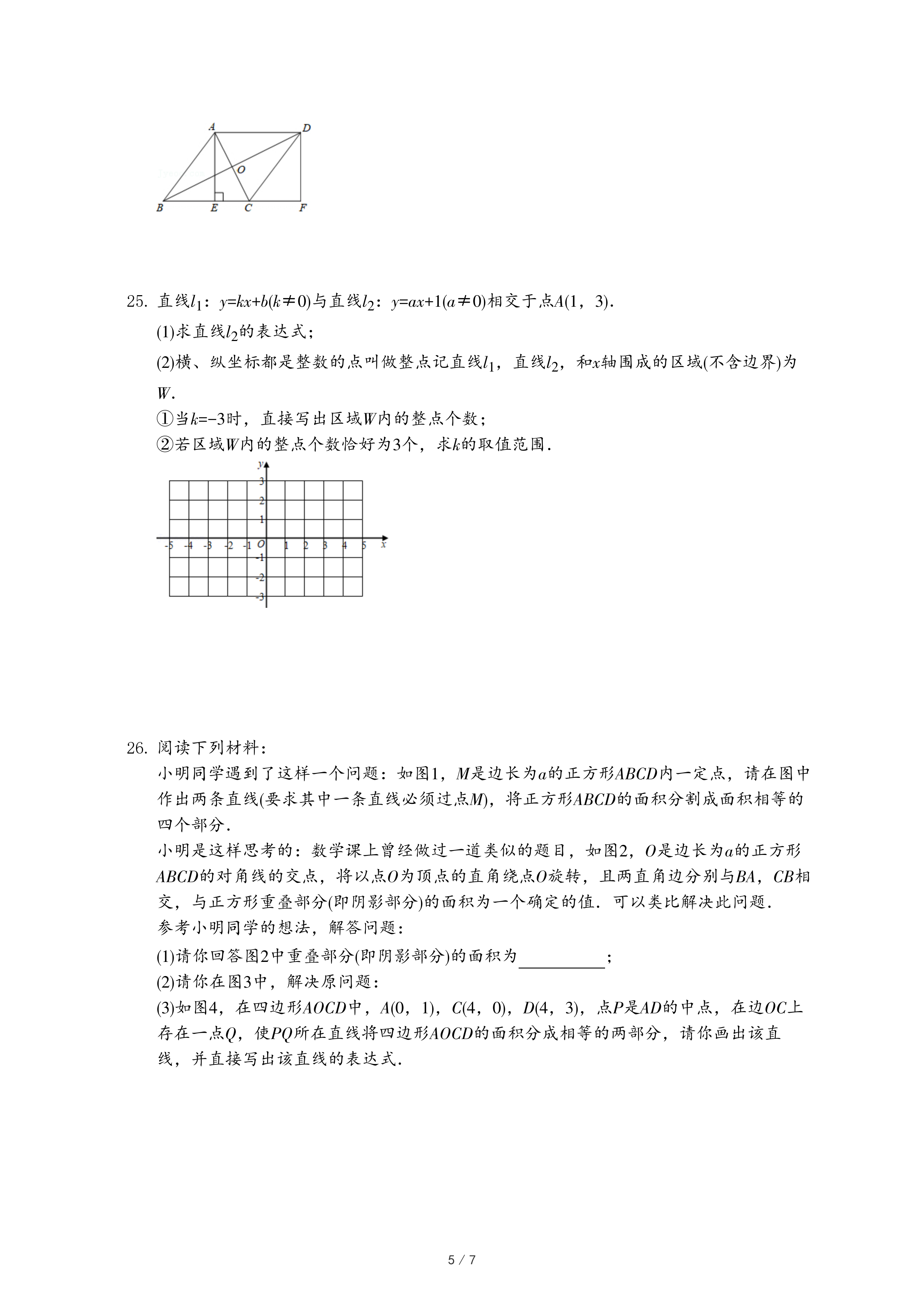
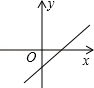
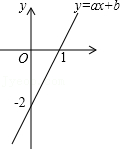
(3)如图4,在四边形AOCD中,A(0,1),C(4,0),D(4,3),点P是AD的中点,在边OC上存在一点Q,使PQ所在直线将四边形AOCD的面积分成相等的两部分,请你画出该直线,并直接写出该直线的表达式.