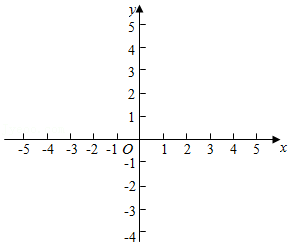28.在平面直角坐标系xOy中,点P的坐标为(x
1,y
1),点Q的坐标为(x
2,y
2),且x
1≠x
2,y
1≠y
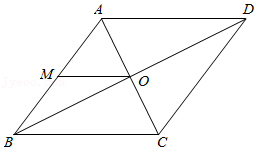
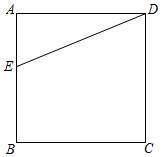
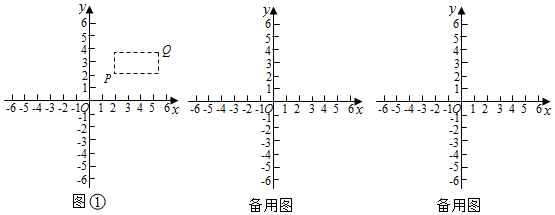
2,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“合成矩形”.如图为点P,Q的“合成矩形”的示意图.
(1)若A点坐标为(2,0),
①当B点坐标为(5,1)时,点A,B的“合成矩形”的面积是
;
②若点C在直线x=4上,且点A,C的“合成矩形”为正方形,求直线AC的表达式;
③若点P在直线y=-2x+2上,且点A,P的“合成矩形”为正方形,直接写出P点的坐标;
(2)点O的坐标为(0,0),点D为直线y=x+b(b≠0)上一动点,若O,D的“合成矩形”为正方形,且此正方形面积不小于2时,求b的取值范围.