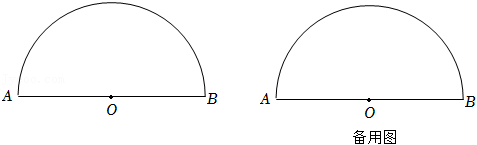
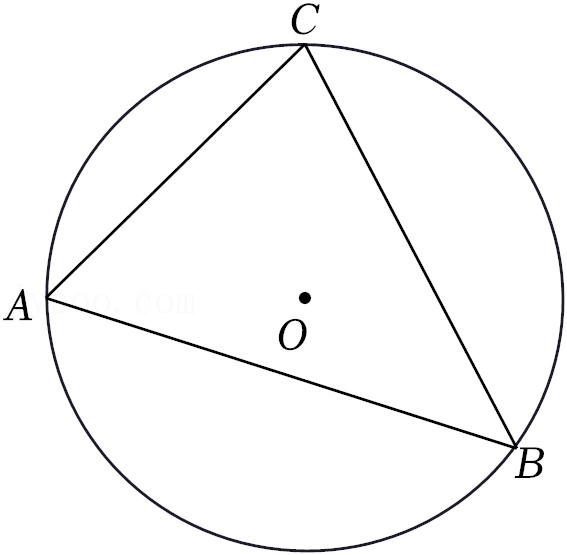
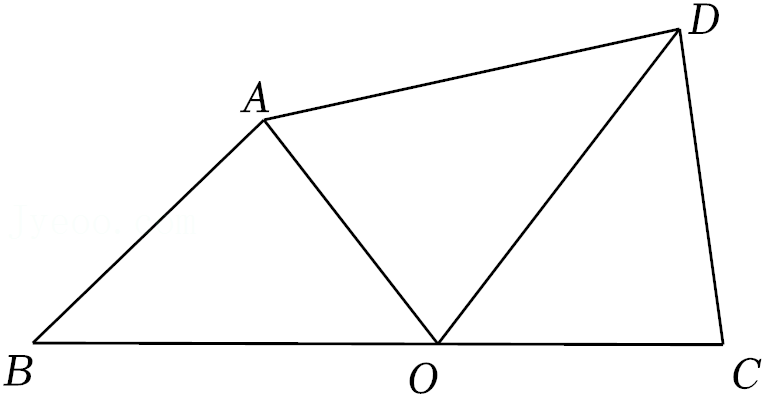
28.现有若干张相同的半圆形纸片,点O是圆心,直径AB的长是12
cm,C是半圆弧上的一点(点C与点A、B不重合),连接AC、BC.
(1)沿AC、BC剪下△ABC,则△ABC是
三角形(填“锐角”、“直角”或“钝角”);
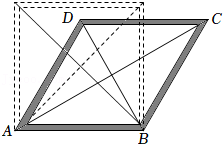
(2)分别取半圆弧上的点E、F和直径AB上的点G、H.已知剪下的由这四个点顺次连接构成的四边形是一个边长为6
cm的菱形.请用直尺和圆规在图中作出一个符合条件的菱形(保留作图痕迹,不要求写作法);
(3)经过数次探索,小明猜想,对于半圆弧上的任意一点C,一定存在线段AC上的点M、线段BC上的点N和直径AB上的点P、Q,使得由这四个点顺次连接构成的四边形是一个边长为4
cm的菱形.小明的猜想是否正确?请说明理由.