26.【经典回顾】
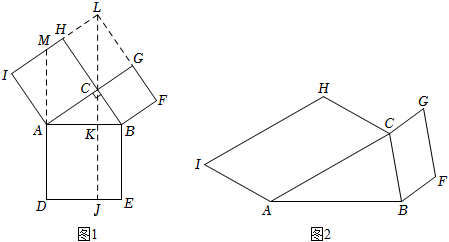
梅文鼎是我国清初著名的数学家,他在《勾股举隅》中给出多种证明勾股定理的方法.图1是其中一种方法的示意图及部分辅助线.
在△ABC中,∠ACB=90°,四边形ADEB、ACHI和BFGC分别是以
Rt△ABC的三边为一边的正方形.延长IH和FG,交于点L,连接LC并延长交DE于点J,交AB于点K,延长DA交IL于点M.
(1)证明:AD=LC;
(2)证明:正方形ACHI的面积等于四边形ACLM的面积;
(3)请利用(2)中的结论证明勾股定理.
【迁移拓展】
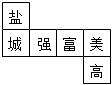
(4)如图2,四边形ACHI和BFGC分别是以△ABC的两边为一边的平行四边形,探索在AB下方是否存在平行四边形ADEB,使得该平行四边形的面积等于平行四边形ACHI、BFGC的面积之和.若存在,作出满足条件的平行四边形ADEB(保留适当的作图痕迹);若不存在,请说明理由.