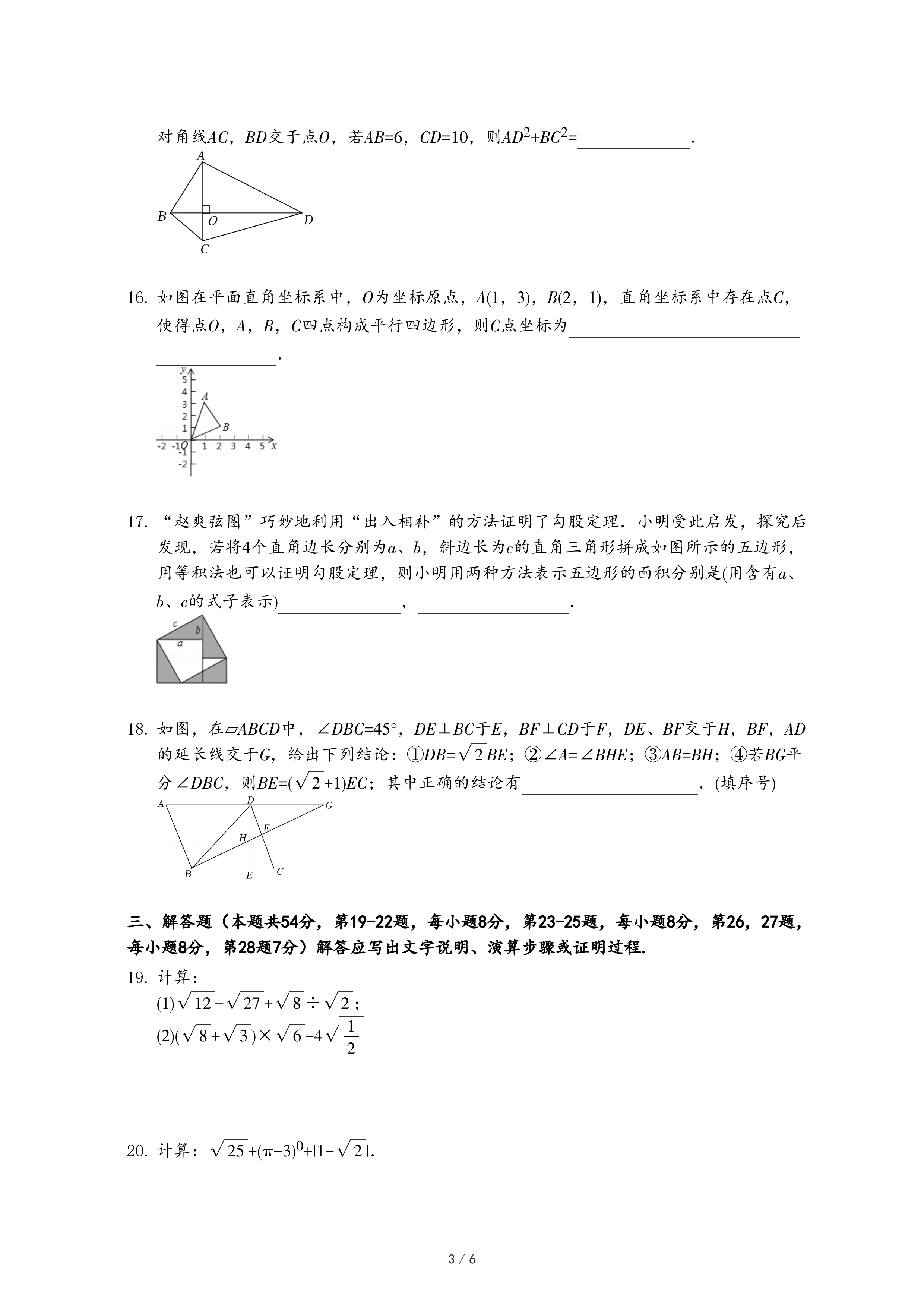
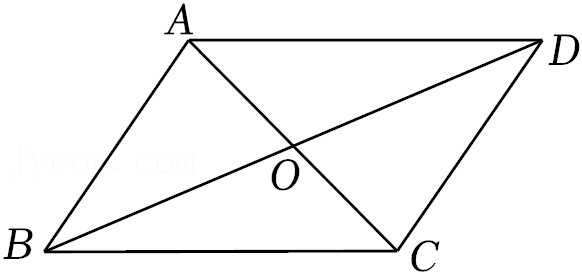
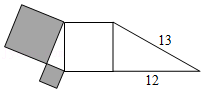
27.数学教育家波利亚曾说:“对一个数学问题,改变它的形式,变换它的结构,直到发现有价值的东西,这是数学解题的一个重要原则”.
材料一:平方运算和开平方运算是互逆运算.如a
2±2ab+b
2=(a±b)
2,那么
√a2±2ab+b2
=|a±b|.如何将双重二次根式
化简?我们可以把5±2
√6
转化为(
√3
)
2±2
√6
+(
√2
)
2=(
√3
±
√2
)
2完全平方的形式,因此双重二次根式
=
=
√3
±
√2
得以化简.
材料二:在直角坐标系xOy中,对于点P(x,y)和Q(x,y')给出如下定义:
若y′=
,则称点Q为点P的“横负纵变点”.例:点(3,2)的“横负纵变点”为(3,2),点(-2,5)的“横负纵变点”为(-2,-5).
请选择合适的材料解决下面的问题:
(1)点(
√2
,-
√3
)的“横负纵变点”为
,
点(-3
√3
,-2)的“横负纵变点”为
;
(2)化简:
=
;
(3)已知a为常数(1≤a≤2),点M(-
√2
,m)且m=
(
+
),点M'是点M的“横负纵变点”,则点M'的坐标是
.