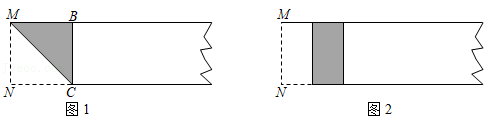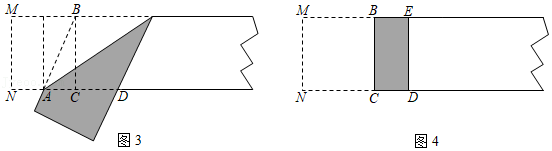19.阅读以下材料,并按要求完成相应的任务:
三角形中位线定理的证明
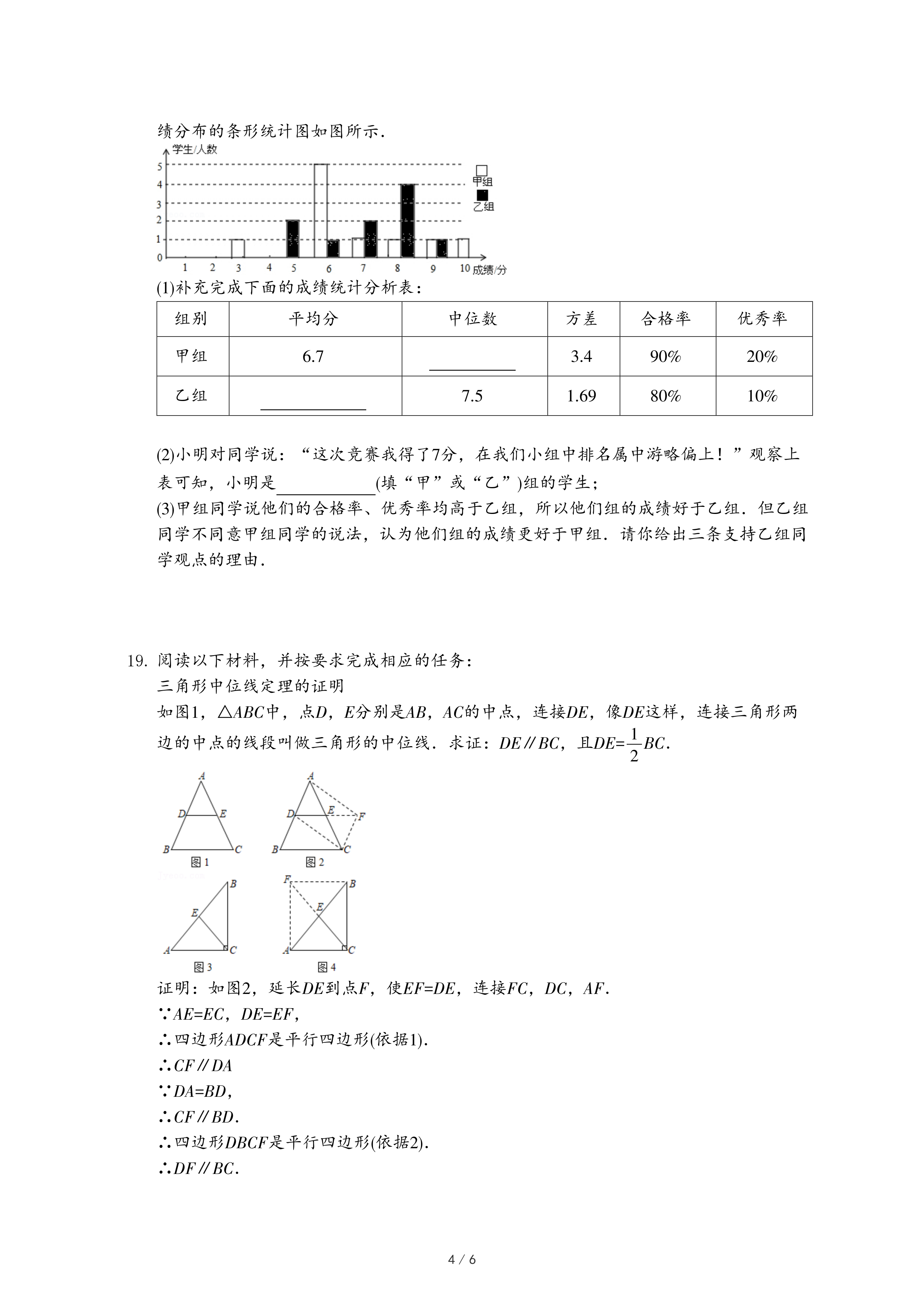
如图1,△ABC中,点D,E分别是AB,AC的中点,连接DE,像DE这样,连接三角形两边的中点的线段叫做三角形的中位线.求证:DE∥BC,且DE=
BC.
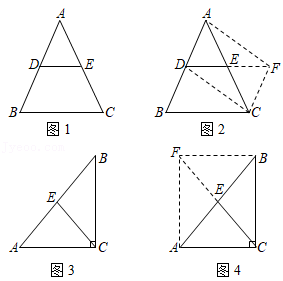
证明:如图2,延长DE到点F,使EF=DE,连接FC,DC,AF.
∵AE=EC,DE=EF,
∴四边形ADCF是平行四边形(依据1).
∴CF∥DA
∵DA=BD,
∴CF∥BD.
∴四边形DBCF是平行四边形(依据2).
∴DF∥BC.
∵DE=
DF,
∴DE∥BC,且DE=
BC.
归纳总结:
上述证明过程中运用了“倍长线段法”,也有人称材料中的方法为“倍长法”(延长了三角形中位线的一倍),该方法是解决初中数学几何题的一种常用方法.
任务(1)
上述材料证明过程中的“依据1”是指:
;
“依据2”是指:
;
类比探究
数学学习小组发现还可以用“倍长线段法”证明定理:直角三角形斜边上的中线等于斜边的一半.
已知:如图3,在
Rt△ACB中,∠ACB=90°,E为AB边的中点,求证:CE=
AB.
证明:延长CE到点F,使EF=CE,连接BF,AF,如图4.
任务(2)请将证明过程补充完整.