22.阅读下列材料,完成相应的任务:
全等四边形
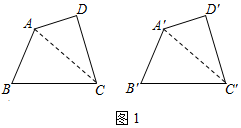
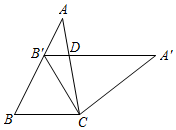
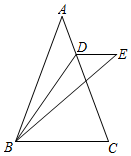
根据全等图形的定义可知:四条边分别相等、四个角也分别相等的两个四边形全等.在“探索三角形全等的条件”时,我们把两个三角形中“一条边相等”或“一个角相等”称为一个条件.智慧小组的同学类比“探索三角形全等条件”的方法探索“四边形全等的条件”,进行了如下思考:如图1,四边形ABCD和四边形A'B'C'D'中,连接对角线AC,A'C',这样两个四边形全等的问题就转化为“△ABC≌△A'B'C'”与“△ACD≌△A'C'D'”的问题.若先给定ABC≌△A'B'C'的条件,只要再增加2个条件使“△ACD≌△A'C'D'”即可推出两个四边形中“四条边分别相等、四个角也分别相等”,从而说明两个四边形全等.
按照智慧小组的思路,小明对图1中的四边形ABCD与四边形A'B'C'D'先给出如下条件:AB=A'B',∠B=∠B′,BC=B'C'.小亮在此基础上又给出“AD=A'D',CD=C'D'”两个条件,他们认为满足这五个条件能得到“四边形ABCD≌四边形A'B'C'D'
(1)请根据小明和小亮给出的条件,说明“四边形ABCD≌四边形A'B'C'D'的理由:
(2)请从下面A,B两题中任选一题作答,我选择
题.
A.在材料中“小明所给条件”的基础上,小颖又给出两个条件“AD=A'D'“∠BCD=∠B'C'D'”.满足这五个条件
(填“能”或“不能”)得到四边形ABCD≌四边形A'B'C'D'
B.在材料中“小明所给条件”的基础上,再添加两个关于原四边形的条件(要求:不同于小亮的条件),使四边形ABCD≌四边形AB'C'D'.你添加的条件是①
,②
.