
















| x0 |
√x+1 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 支付金额a(元) | 0<a≤1000 | 1000<a≤2000 | a>2000 |
| 仅使用A | 36人 | 18人 | 6人 |
| 仅使用B | 20人 | 28人 | 2人 |
| 6000 |
| x |
| 4500 |
| x+500 |
| 6000 |
| x-500 |
| 4500 |
| x |
| 6000 |
| x |
| 4500 |
| x-500 |
| 6000 |
| x+500 |
| 4500 |
| x |
| 5 √3 |
| 2 |
| 5 |
| 2 |
| 3 √5 |
| 2 |
| 9 |
| 4 |
| 7 |
| 2 |
| 5 |
| 2 |
| 3 √13 |
| 4 |
| x+3 |
| x2-3x |
| x-1 |
| x2-6x+9 |
| x-9 |
| x |
| 2 |
| 5 |
| 1 |
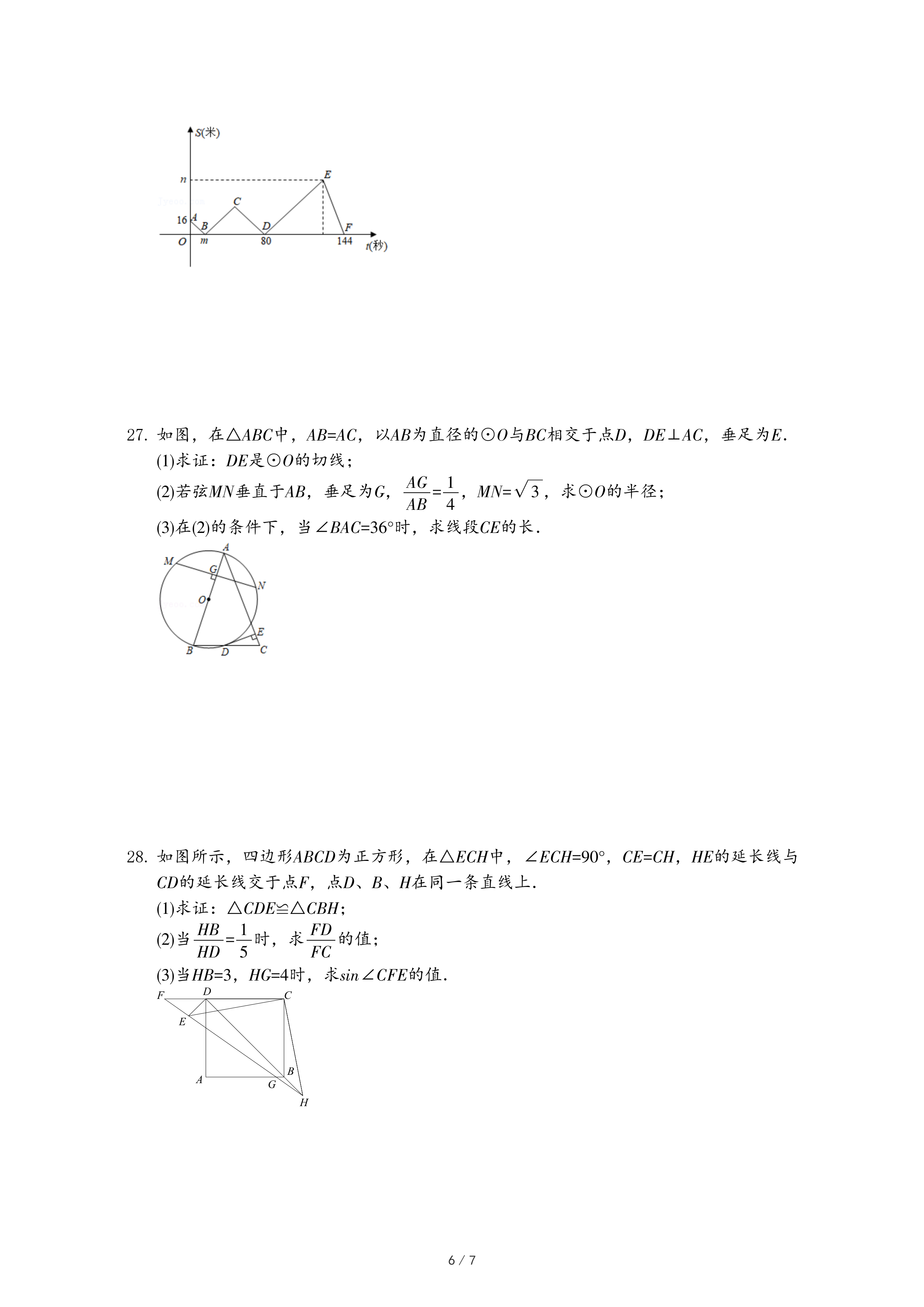
| m |
| 1 |
| n |
| k |
| x |

| 1 |
| 2 |
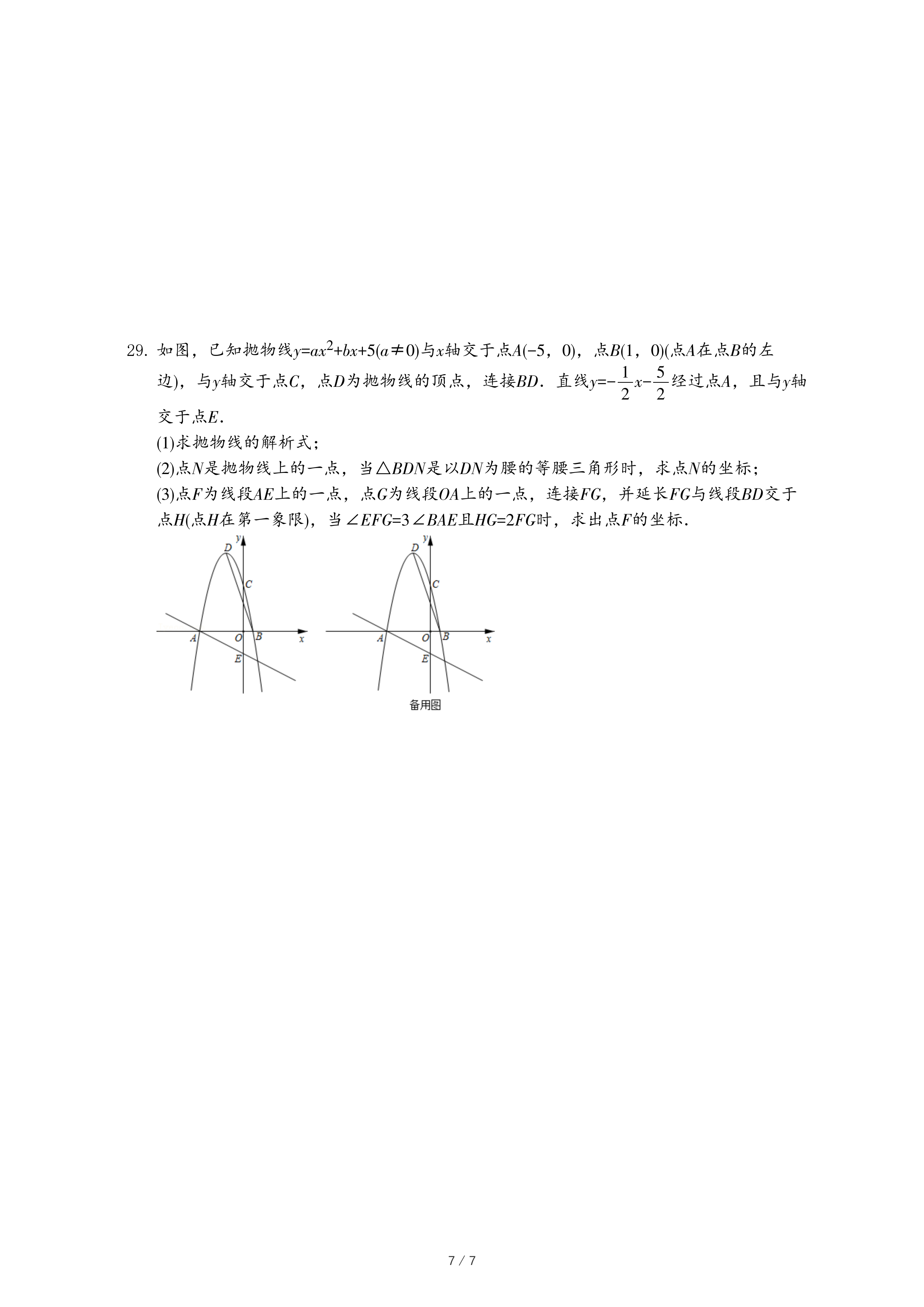
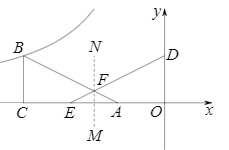
| AG |
| AB |
| 1 |
| 4 |
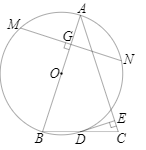
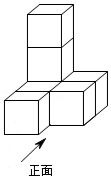
| HB |
| HD |
| 1 |
| 5 |
| FD |
| FC |
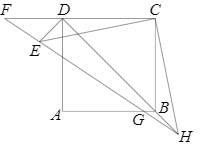
| 1 |
| 2 |
| 5 |
| 2 |