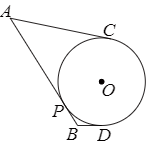
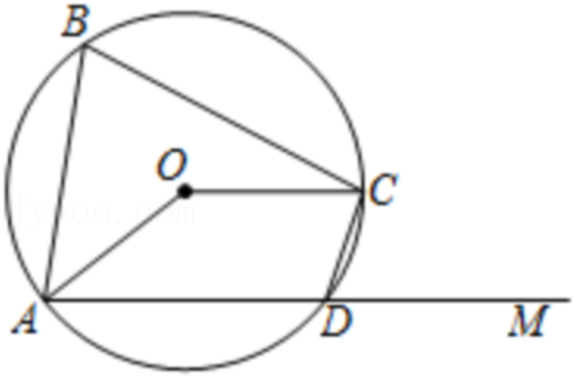
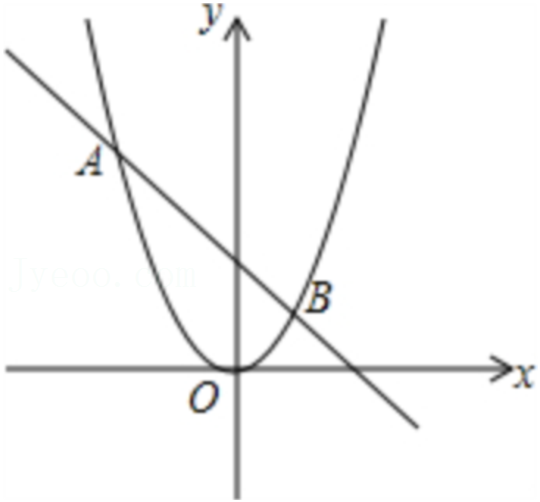
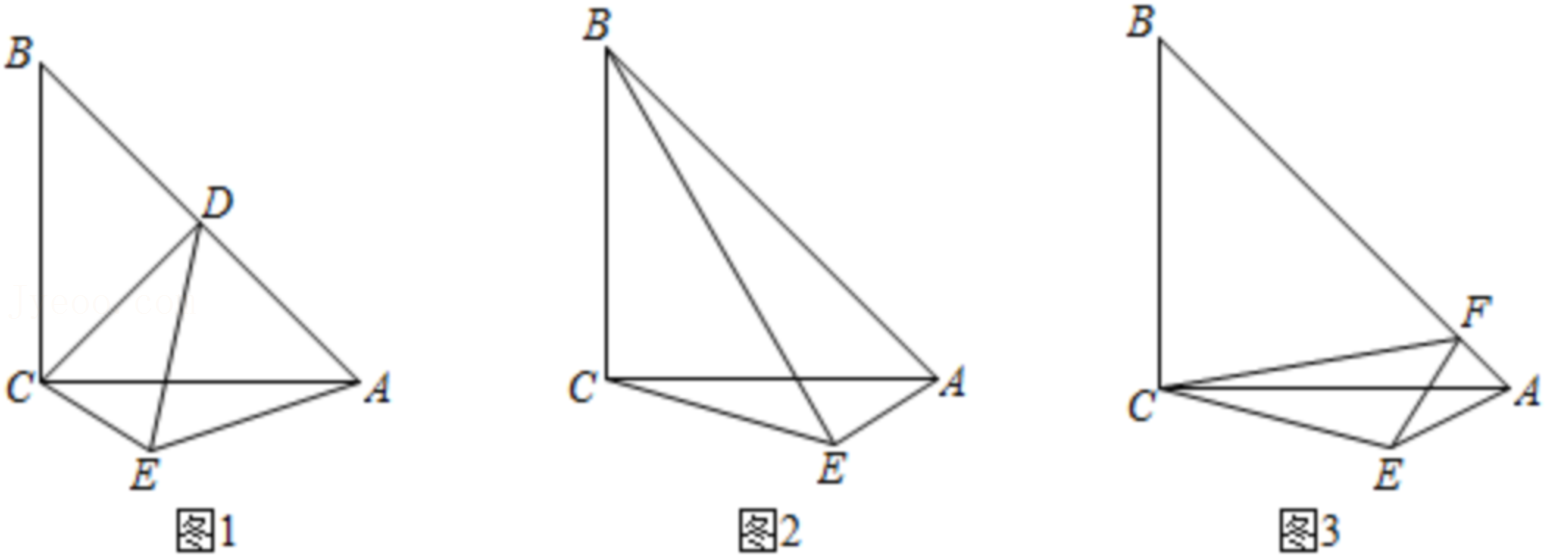
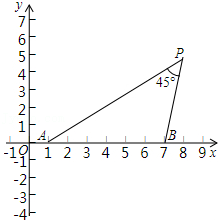28.在平面直角坐标系xOy中,给定⊙C,若将线段AB绕原点O逆时针旋转α(0°<α<180°),使得旋转后对应的线段A′B′所在直线与⊙C相切,并且切点P在线段A′B′上,则称线段AB是⊙C的旋转切线段,其中满足题意的最小的α称为关于⊙C和线段AB的最小旋转角.
已知C(0,2),⊙C的半径为1.
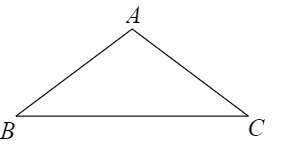
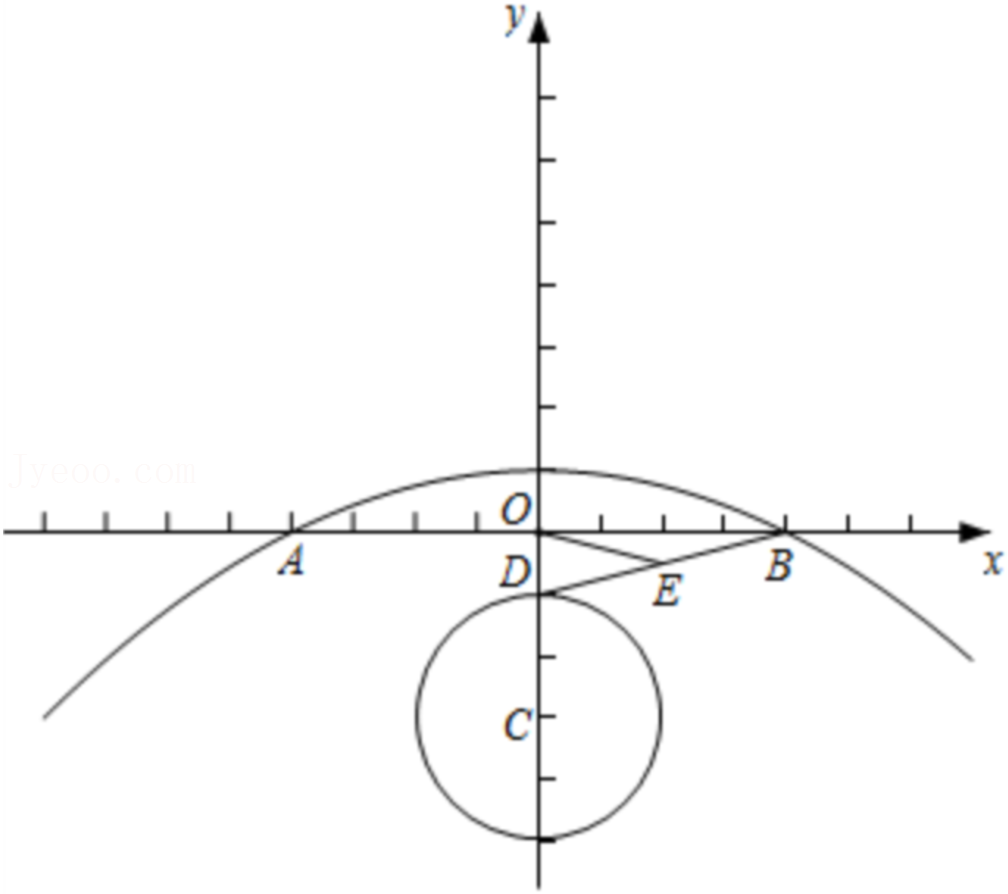
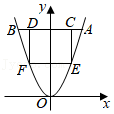
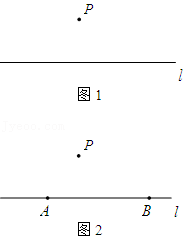
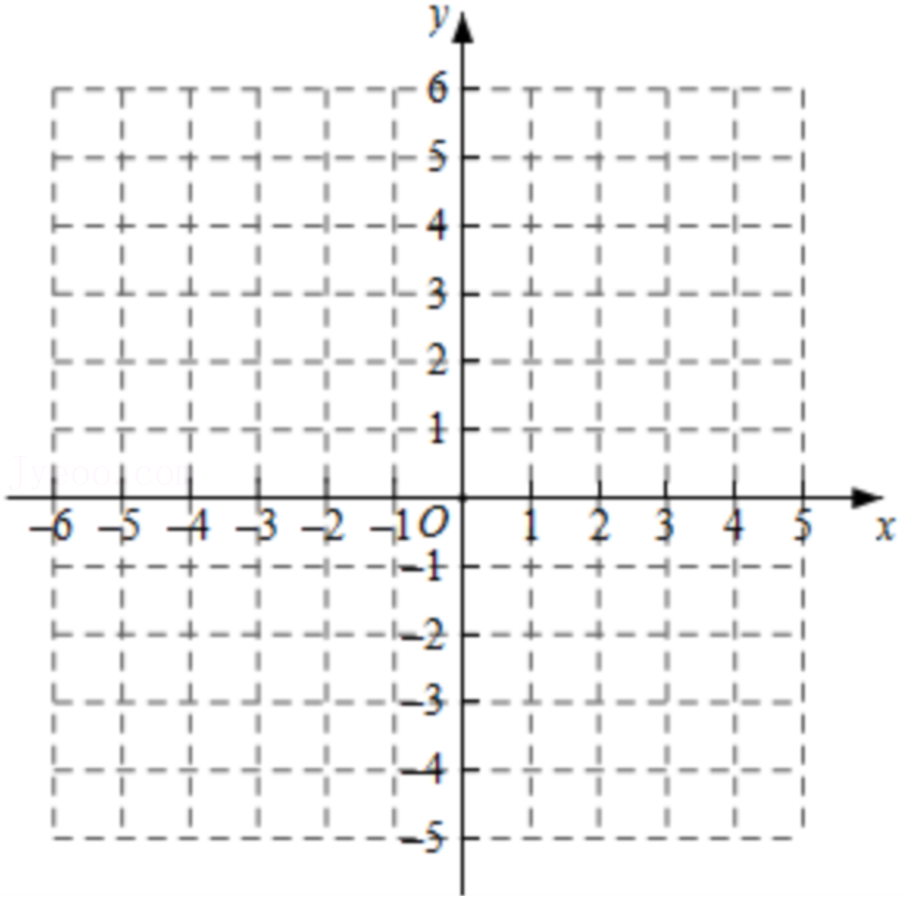
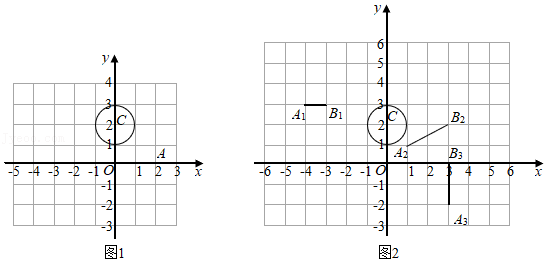
(1)如图1,A(2,0),线段OA是⊙C的旋转切线段,写出关于⊙C和线段OA的最小旋转角为
°;
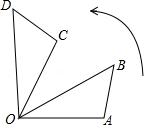
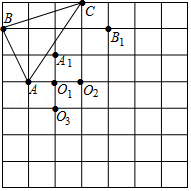
(2)如图2,点A
1,B
1,A
2,B
2,A
3,B
3的横、纵坐标都是整数.在线段A
1B
1,A
2B
2,A
3B
3中,⊙C的旋转切线段是
;
(3)已知B(1,0),D(t,0),若线段BD是⊙C的旋转切线段,求t的取值范围;
(4)已知点M的横坐标为m,存在以M为端点,长度为
√3
的线段是⊙C的旋转切线段,直接写出m的取值范围.




 科克曲线
科克曲线 笛卡尔心形线
笛卡尔心形线 赵爽弦图
赵爽弦图 斐波那契螺旋线
斐波那契螺旋线