17．解方程：
(1)x²-4x-6=0；
(2)(x-1)²+2x(x-1)=0．

18．如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A(-2，4)，B(-4，2)，C(-1，1)(每个小方格都是边长为1个单位长度的正方形)．请完成以下画图并填空．
(1)画出△ABC关于原点O成中心对称的△A₁B₁C₁(点A，B，C的对应点分别为A₁，B₁，C₁)；
(2)将△ABC绕点O顺时针旋转90°，画出旋转后得到的△A₂B₂C₂(点A，B，C的对应点分别为A₂，B₂，C₂)；
(3)△ABC的面积为       ．(直接填结果)

19．先阅读以下材料，再解答问题：
在学习了一元二次方程的解法后，利用课后托管时间，数学兴趣小组的同学对一元四次方程x⁴-5x²+4=0的解法进行了如下探究：根据该方程的特点，可以把x²视为一个整体，然后设x²=y，则x⁴=y²，原方程可化为y²-5y+4=0①，解得y₁=1，y₂=4．
当y=1时，x²=1，∴x=±1；
当y=4时，x²=4，∴x=±2．
∴原方程的解为x₁=1，x₂=-1，x₃=2，x₄=-2．
请解答问题：
(1)填空：在由原方程得到方程①的过程中，主要利用       法达到了降次的目的，体现了       的数学思想；
(2)仿照以上方法解方程：(x²-x)²+(x²-x)-6=0．

20．如图，用一段长为30m的篱笆围成一个一边靠墙的矩形菜园CDEF，墙长AB为8m．
(1)设DE=xm，求出菜园面积y与x之间的函数关系式，并写出自变量x的取值范围；
(2)DE的长为多少时，菜园的面积最大？最大面积是多少？

21．已知关于x的一元二次方程x²+(2m-1)x+m²-2=0有两个实数根x₁，x₂．
(1)求实数m的取值范围；
(2)当m=1时，求代数式(x₁²+2x₁)(x₂²-2)的值．

22．如图，在矩形ABCD中，AB=10cm，BC=12cm，点P从点A开始沿边AB向终点B以2cm/s的速度移动，点Q从点B开始沿边BC向终点C以4cm/s的速度移动．如果点P，Q分别从点A，B同时出发，当点Q运动到点C时，两点都停止运动．设运动时间为ts(t＞0)．
(1)线段BQ=      cm，PB=      cm；(用含t的代数式表示)
(2)当t为何值时，PQ的长为4cm？
(3)是否存在t，使得五边形APQCD的面积等于99cm²？若存在，请求出此时t的值；若不存在，请说明理由．

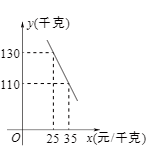
23．金秋十月，梁子湖区成功获评“国家生态文明建设示范区”，以生态环境保护与绿色经济共赢的特色吸引各地游客纷纷前来观光．梁湖超市销售一批成本为20元/千克的绿色健康食品，深受游客青睐．经市场调查发现，该食品每天的销售量y(千克)与销售单价x(元/千克)之间满足一次函数关系，其图象如图所示．
(1)求该食品每天的销售量y(千克)与销售单价x(元/千克)之间的函数关系式；
(2)若超市按售价不低于成本价，且不高于40元销售，则销售单价定为多少，才能使销售该食品每天获得的利润W(元)最大？最大利润是多少？
(3)若超市要使每天销售该食品获得的利润不低于2400元，则每天的销售量最少应为多少千克？

24．如图，在平面直角坐标系xOy中，抛物线y=x²+2x-3与x轴交于点A和点B(点A在点B的左侧)，顶点为D．直线l与抛物线交于B，C两点，其中点C的横坐标为-2．
(1)直接写出点A，B，C，D的坐标：
点A      ，点B      ，点C      ，点D      ；
(2)直线l与抛物线的对称轴交于点E，P为线段BC上一动点(点P不与点B，C重合)，过点P作PF∥DE交抛物线于点F，设点P的横坐标为t．
①用含t的代数式表示线段PF的长，并求出t为何值时，四边形PEDF是平行四边形；
②设△BCF的面积为S，当t为何值时，S最大？最大值是多少？