





| 1 |
| 2 |
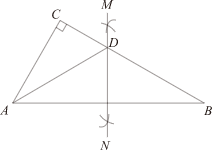

| { | y=x+4.5 0.5y=x-1 |
| { | y=x+4.5 y=2x-1 |
| { | y=x-4.5 0.5y=x+1 |
| { | y=x-4.5 y=2x-1 |
√5 |
| 5 |
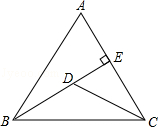
| { | x+1≥0 3x-6<0 |
| 摸球实验次数 | 100 | 1000 | 5000 | 10000 | 50000 | 100000 |
| "摸出黑球"的次数 | 36 | 387 | 2019 | 4009 | 19970 | 40008 |
| "摸出黑球"的频率(结果保留小数点后三位) | 0.360 | 0.387 | 0.404 | 0.401 | 0.399 | 0.400 |
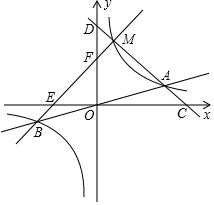
| k |
| x |
| 2 |
| 5 |
| 1 |
| 2 |
| a+3 |
| a-1 |
| 1 |
| a-1 |
| a2+4a+4 |
| a2-a |
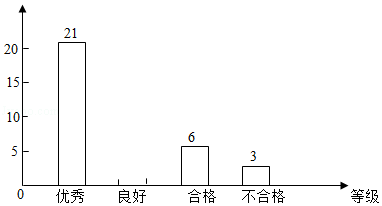
| 等级 | 频数 | 频率 |
| 优秀 | 21 | 42% |
| 良好 | m | 40% |
| 合格 | 6 | n% |
| 待合格 | 3 | 6% |
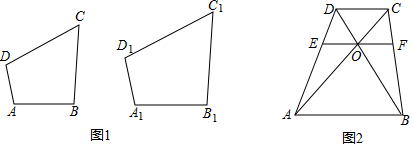
| AB |
| A1B1 |
| BC |
| B1C1 |
| CD |
| C1D1 |
| S2 |
| S1 |
| m |
| 2m+1 |
| 1 |
| y+2 |
| n |
| 2n+1 |
√3 |
| 3 |
| 1 |
| OD |
| 1 |
| OE |
