23.在学习了平行线的有关知识后,小明对下面的问题进行了研究.
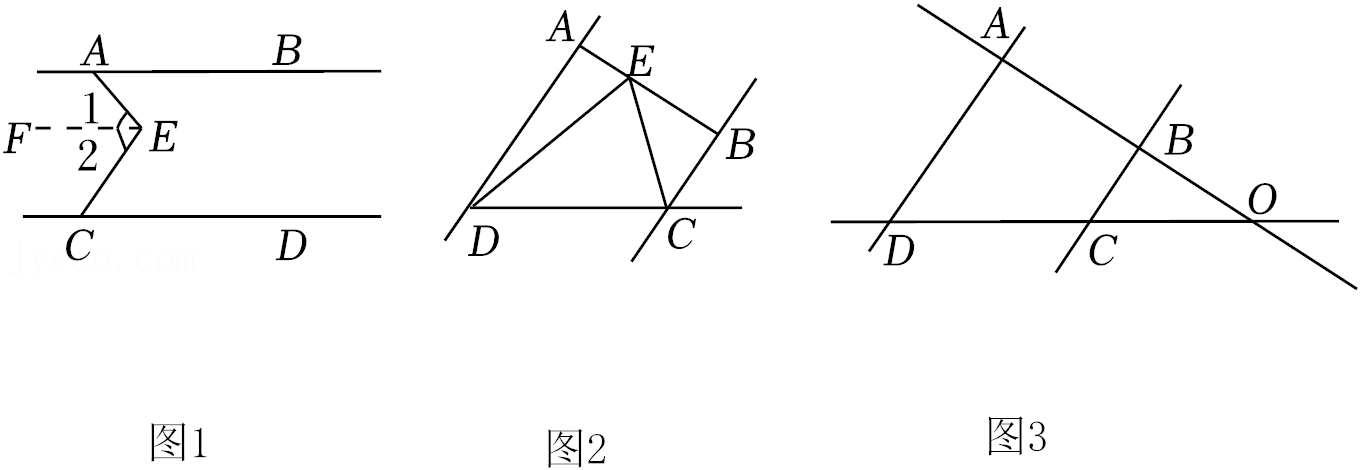
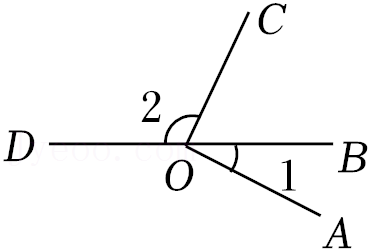
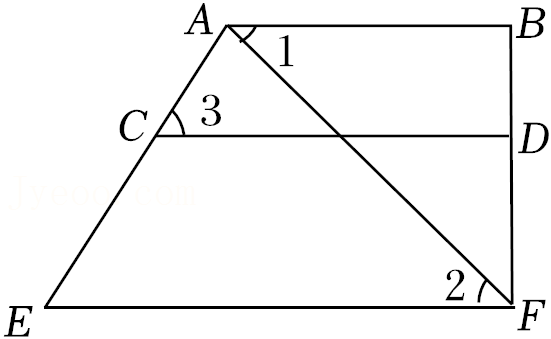
问题:如图1,AB∥CD,点E在直线AB与CD之间,连结AE,CE,
试说明∠BAE+∠DCE=∠AEC.
(1)下面是小明的解题过程,请你填空.
解:过点E作EF∥AB,
∴∠BAE=∠1(
).
∵CD∥AB(已知),
∴EF∥CD(
).
∴∠DCE=∠2(两直线平行,内错角相等).
∴∠BAE+∠DCE=∠1+∠2(等式的性质).
∴∠BAE+∠DCE=∠AEC(等量代换).
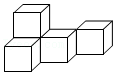
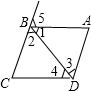
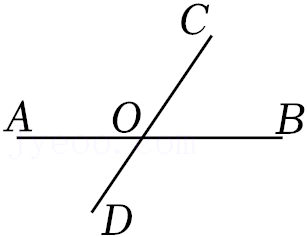
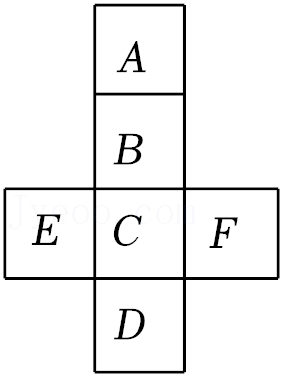
(2)如图2,AD∥BC,点E在线段AB上运动(点E不与点A,B重合),连结CE,DE,若∠ADE=α,∠BCE=β.试说明∠CED,α,β之间的数量关系(写出过程,不需要注明依据).
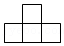
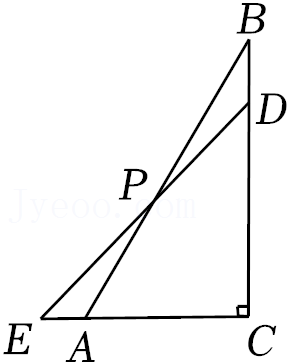
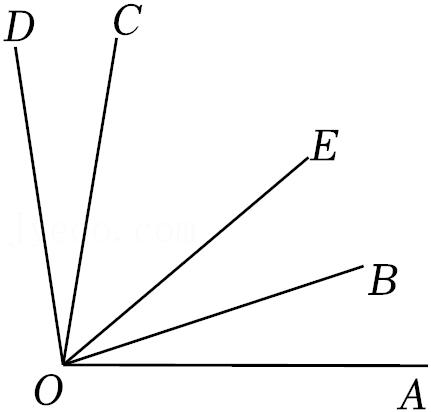
(3)如图3,AD∥BC,点E在直线AB上运动(点E不与点A,B,O重合),连结CE,DE,若∠ADE=α,∠BCE=β,则∠CED,α,β之间的数量关系是
.