
| { | x-y=3 3x-8y=14 |
| { | x=-1 y=2 |
| { | x=1 y=-2 |
| { | x=-2 y=1 |
| { | x=2 y=-1 |
| a2+b2 |
| 2a |
| a |
| a-b |
| 公交车用时公交车用时的频数线路 | 30≤t≤35 | 35<t≤40 | 40<t≤45 | 45<t≤50 | 合计 |
| A | 59 | 151 | 166 | 124 | 500 |
| B | 50 | 50 | 122 | 278 | 500 |
| C | 45 | 265 | 167 | 23 | 500 |
| 船型 | 两人船(限乘两人) | 四人船(限乘四人) | 六人船(限乘六人) | 八人船(限乘八人) |
| 每船租金(元/小时) | 90 | 100 | 130 | 150 |
| { | 3(x+1)>x−1
|
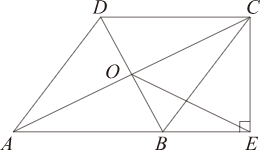
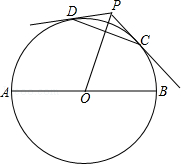
| k |
| x |
| 1 |
| 4 |
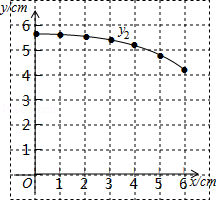
| x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y1/cm | 5.62 | 4.67 | 3.76 | 2.65 | 3.18 | 4.37 | |
| y2/cm | 5.62 | 5.59 | 5.53 | 5.42 | 5.19 | 4.73 | 4.11 |
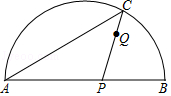
| 课程 | 平均数 | 中位数 | 众数 |
| A | 75.8 | m | 84.5 |
| B | 72.2 | 70 | 83 |