



| 1 |
| 2019 |
| 1 |
| 2019 |




| a2+1 |
| a+1 |
| 2 |
| a+1 |
| a-1 |
| a+1 |
| 1 |
| a+1 |
| BC |
| B′C′ |
| 4 |
| 3 |
| 16 |
| 9 |
| { | 5x+6y=1 5x-y=6y-x |
| { | 6x+5y=1 5x+y=6y+x |
| { | 5x+6y=1 4x+y=5y+x |
| { | 6x+5y=1 4x-y=5y-x |
| 1 |
| 2 |
√2 |
| 2 |
| k |
| x |
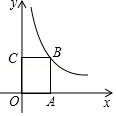
| 1 |
| 2 |
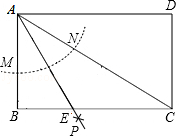
| { | 2x-1<x+5
|
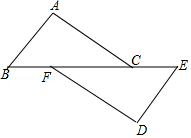
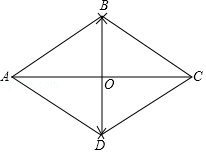
| k |
| x |
| k |
| x |
| 分数段班级 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
| 八年级1班 | 7 | 5 | 10 | 3 |
| 统计量班级 | 平均数 | 中位数 | 众数 | 极差 | 方差 |
| 八年级1班 | 78 | ________ | 85 | 36 | 105.28 |
| 统计量班级 | 平均数 | 中位数 | 众数 | 极差 | 方差 |
| 八年级2班 | 75 | 76 | 73 | 44 | 146.80 |

| x/cm | 0 | 0.30 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 |
| 3.00 | 3.50 | 3.68 | 3.81 | 3.90 | 3.93 | 4.10 | ||
| y/cm | 2.88 | 2.81 | 2.69 | 2.67 | 2.80 | 3.15 | 3.85 | 5.24 | 6.01 | 6.71 | 7.27 | 7.44 | 8.87 |


| 3 |
| 2 |
| 5 |
| 4 |