




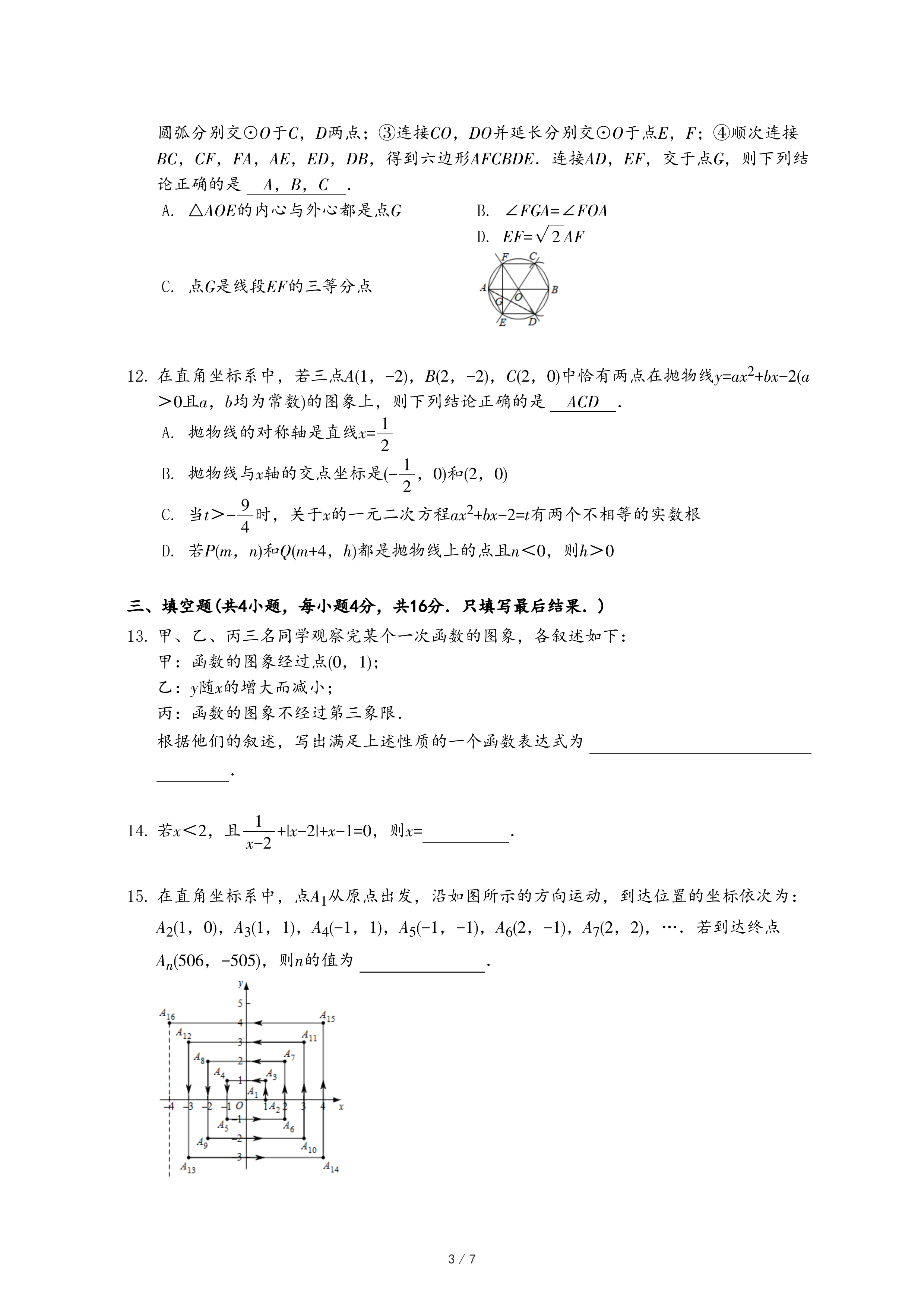

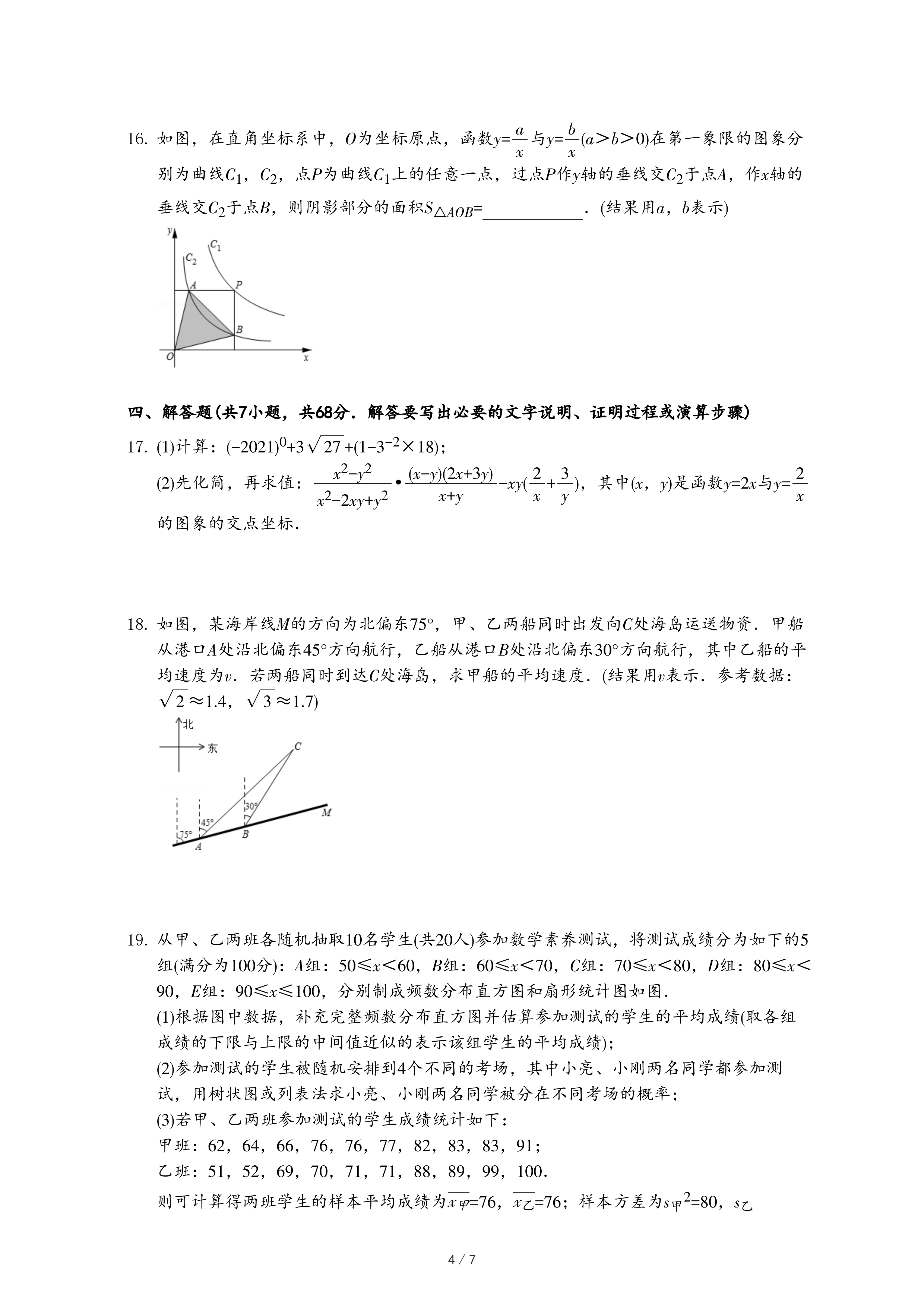

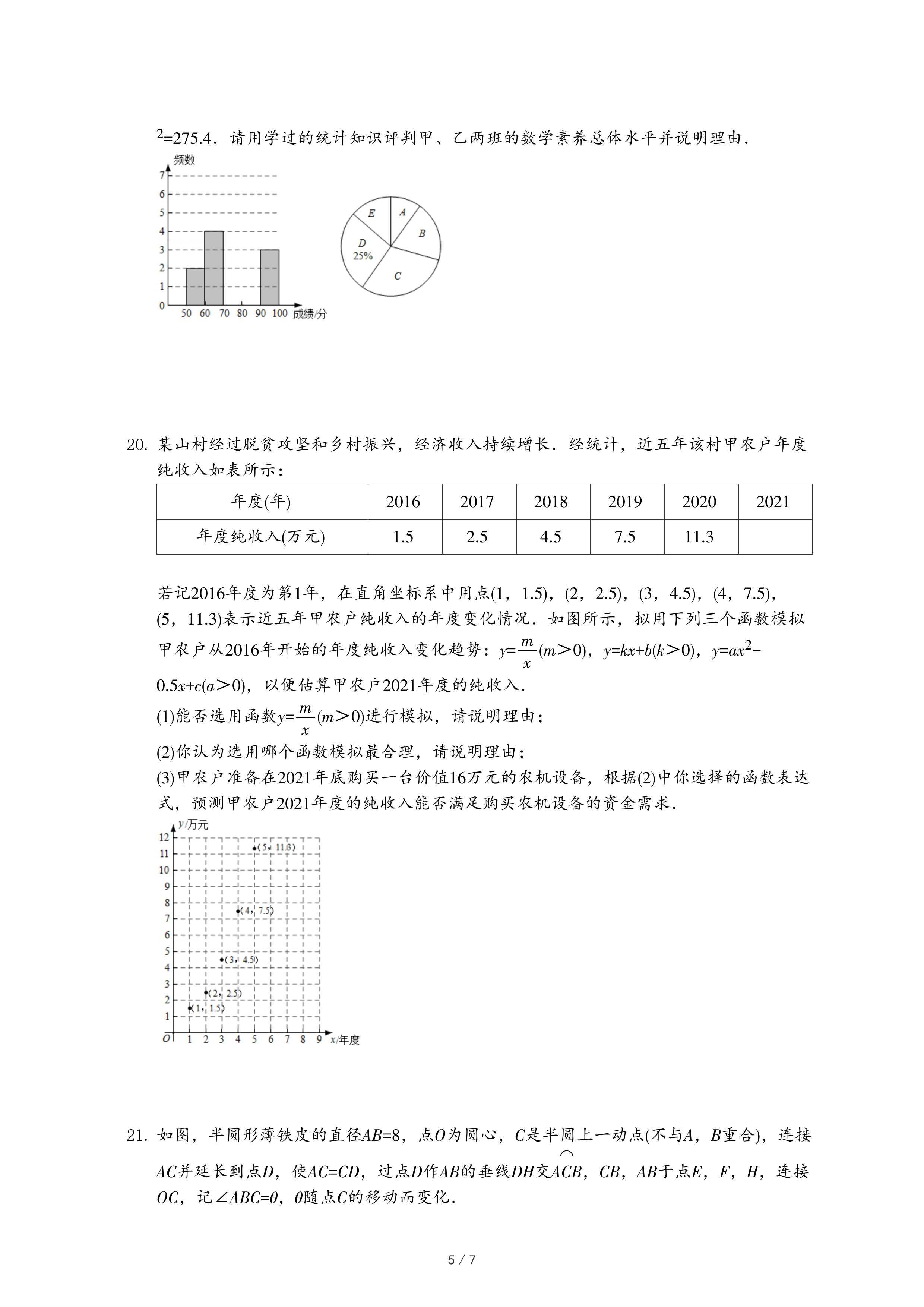

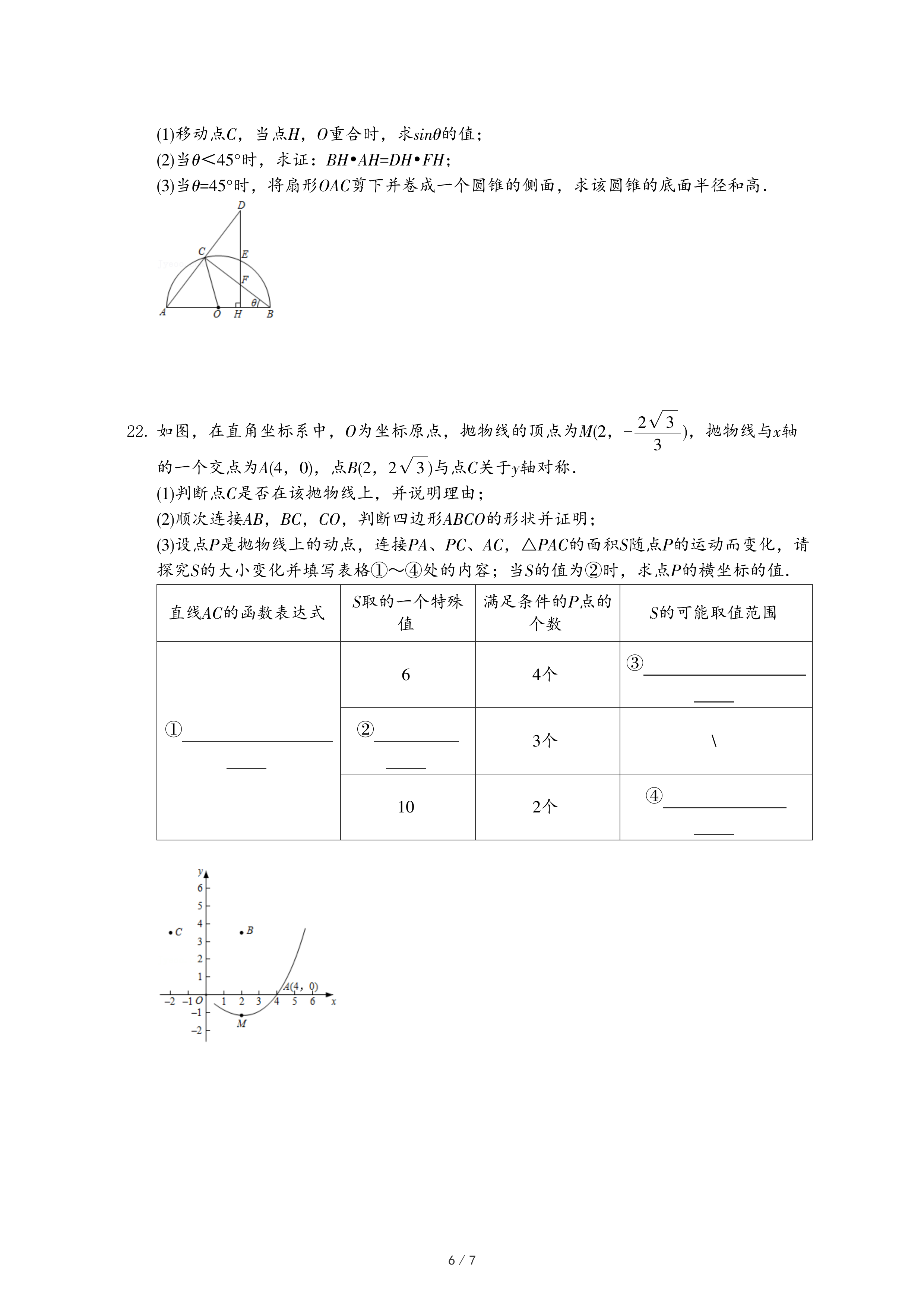

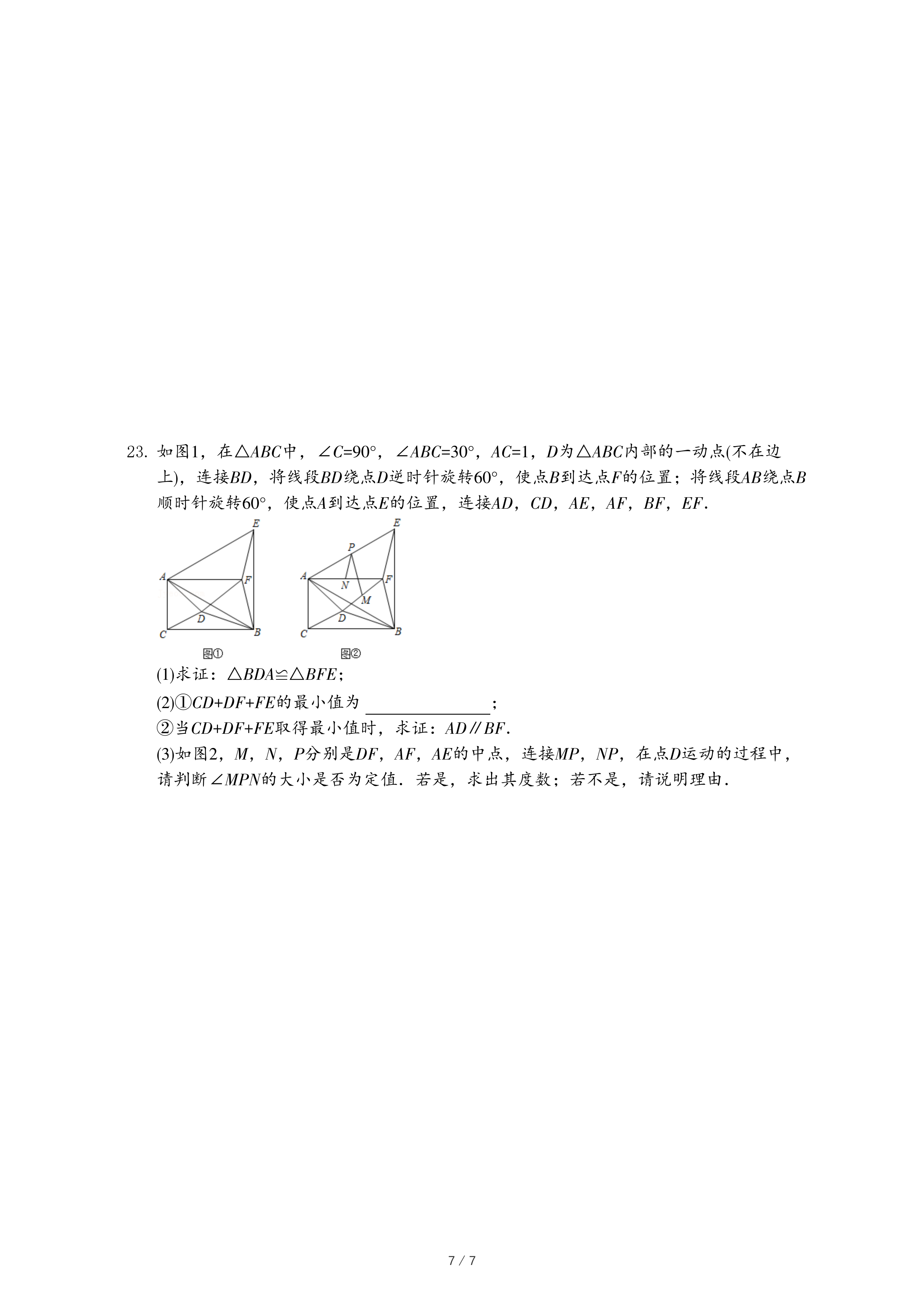

| 3 |
| 2 |


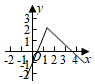
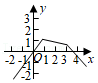
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| a2 |
| a-3 |
| b-3 |
| a |
| b |
√6 |
√3 |
| 1 |
| 3 |
| 1 |
| 5 |
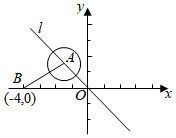
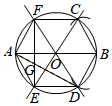
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
| 1 |
| x-2 |
| a |
| x |
| b |
| x |
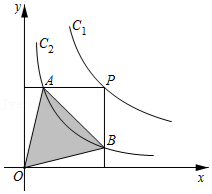
| x2-y2 |
| x2-2xy+y2 |
| (x-y)(2x+3y) |
| x+y |
| 2 |
| x |
| 3 |
| y |
| 2 |
| x |
| 年度(年) | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 |
| 年度纯收入(万元) | 1.5 | 2.5 | 4.5 | 7.5 | 11.3 |
| m |
| x |
| m |
| x |
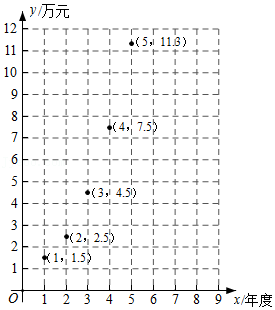
| 2 √3 |
| 3 |
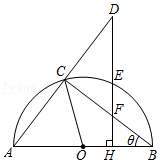
| 直线AC的函数表达式 | S取的一个特殊值 | 满足条件的P点的个数 | S的可能取值范围 |
| ① | 6 | 4个 | ③ |
| ② | 3个 | \ | |
| 10 | 2个 | ④ |