





 科克曲线
科克曲线 笛卡尔心形线
笛卡尔心形线 赵爽弦图
赵爽弦图 斐波那契螺旋线
斐波那契螺旋线| 5 |
| 12 |
| 5 |
| 13 |
| 12 |
| 13 |
| 13 |
| 12 |
| 5 |
| 2 |
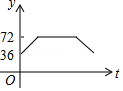
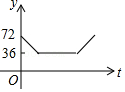
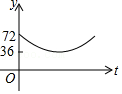
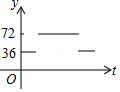
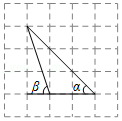
| k |
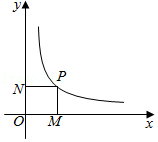
| x |
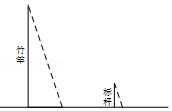
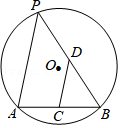
| 投针次数n | 1000 | 2000 | 3000 | 4000 | 5000 | 10000 | 20000 | ||
| 针与直线相交的次数m | 454 | 970 | 1430 | 1912 | 2386 | 4769 | 9548 | ||
针与直线相交的频率p=
| 0.454 | 0.485 | 0.4767 | 0.478 | 0.4772 | 0.4769 | 0.4774 |
| 1 |
| 3 |
| k |
| x |
| k |
| x |
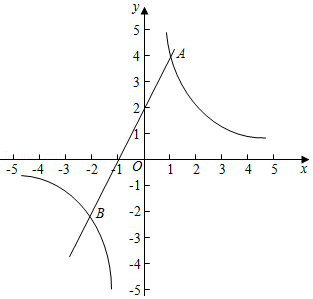


| x | … | -3 | -
| -2 | -
| -1 | -
| 0 |
| 1 |
| 2 |
| 3 | … | ||||||||||||
| y | … | 8 |
| 3 | a | 0 |
| 1 | b | 0 |
| 3 |
| 8 | … |