23.小明进行铅球训练,他尝试利用数学模型来研究铅球的运动情况.他以水平方向为x轴方向,1
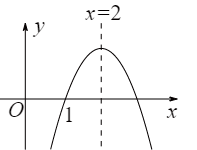
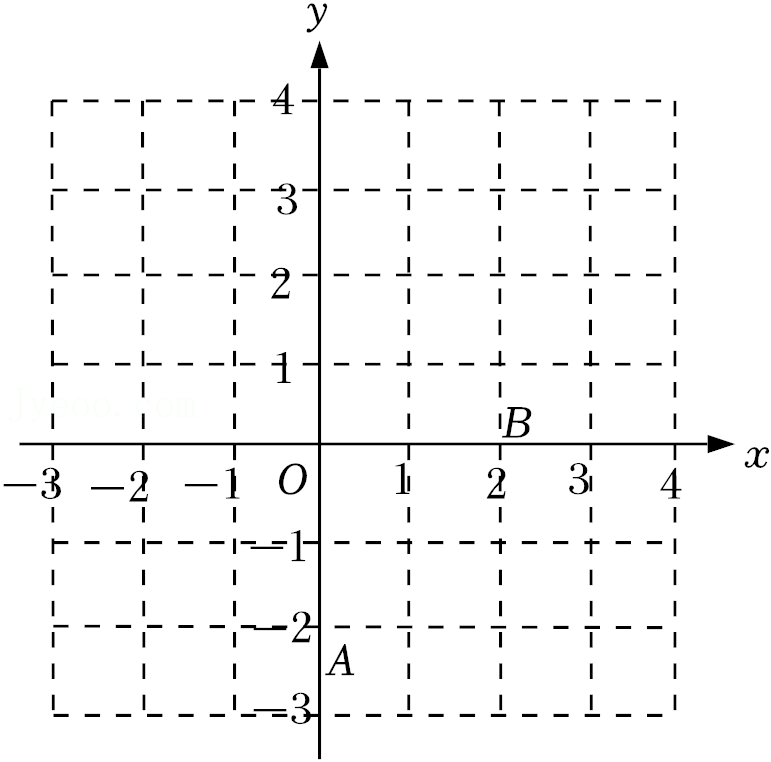
m为单位长度,建立了如图所示的平面直角坐标系,铅球从y轴上的A点出手,运动路径可看作抛物线,在B点处达到最高位置,落在x轴上的点C处.小明某次试投时的数据如图所示.
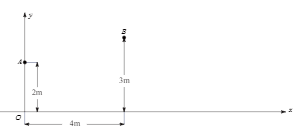
(1)在图中画出铅球运动路径的示意图;
(2)根据图中信息,求出铅球路径所在抛物线的表达式;
(3)若铅球投掷距离(铅球落地点C与出手点A的水平距离OC的长度)不小于10
m,成绩为优秀.请通过计算,判断小明此次试投的成绩是否能达到优秀.