23.阅读材料,回答下列问题:
【问题提出】几何学的产生,源于人们对土地测量的需要,后来由实际问题转换成了数学问题,初中数学常用的几何模型有很多,但是通过整理归纳,就可以从这些基本模型找到其中所蕴含的规律.
【问题解决】
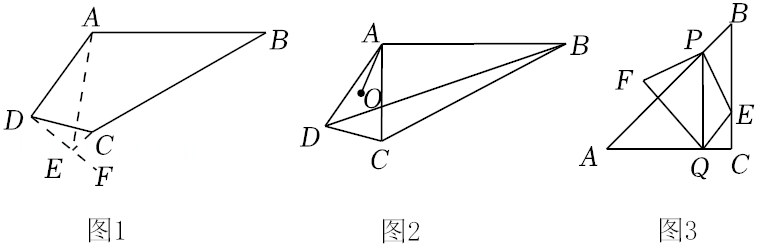
(1)如图1,在四边形ABCD中,∠ABC+∠ADC=90°,∠CDF=∠ABC,过点C作CE⊥DF于点E,连接AE,发现AD,DE,AE之间的数量关系是
;
【问题探究】
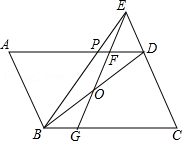
如图2,在四边形ABCD中,连接AC,∠BAC=90°,点O是△ACD两边垂直平分线的交点,连接OA,∠OAC=∠ABC.
(2)探究一:∠ABC与∠ADC之间有怎样的数量关系?请说明理由;
(3)探究二:连接BD,已知AD=m,DC=n,
=2,求BD的长(用含m,n的式子表示).
【拓展延伸】
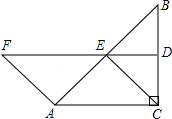
如图3,
Rt△ABC中,∠C=90°,AC=BC,点P为边AB上一点(不与A、B重合),过P作PQ⊥AC于Q,做QE∥AB交BC于点E,连接PE,将线段PE绕点P顺时针旋转90°到PF,连接QF,
(4)拓展一:线段FQ、EQ、AP之间有怎样的数量关系?请说明理由;
(5)拓展二:若PE=
AC,求
的值是
.