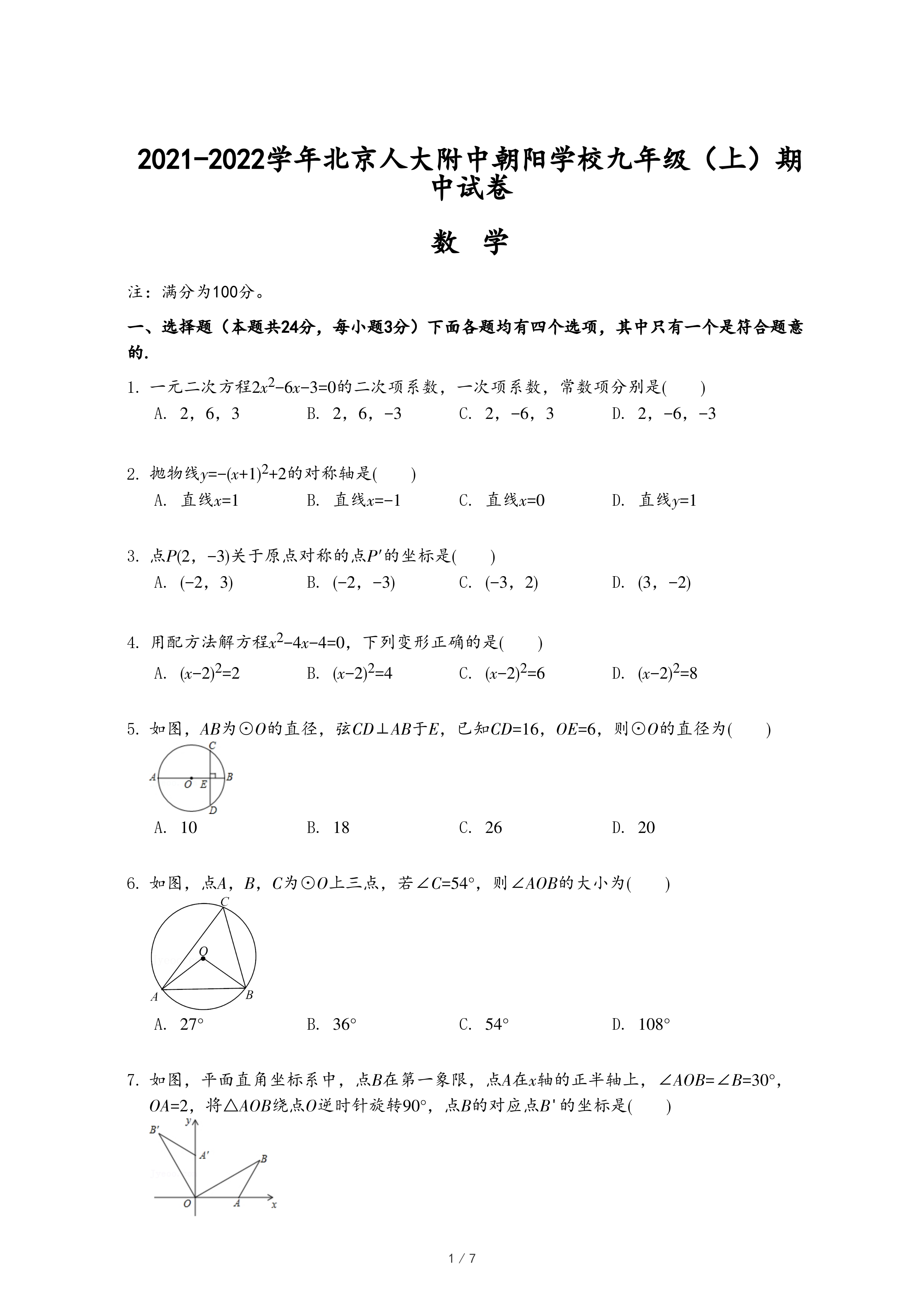
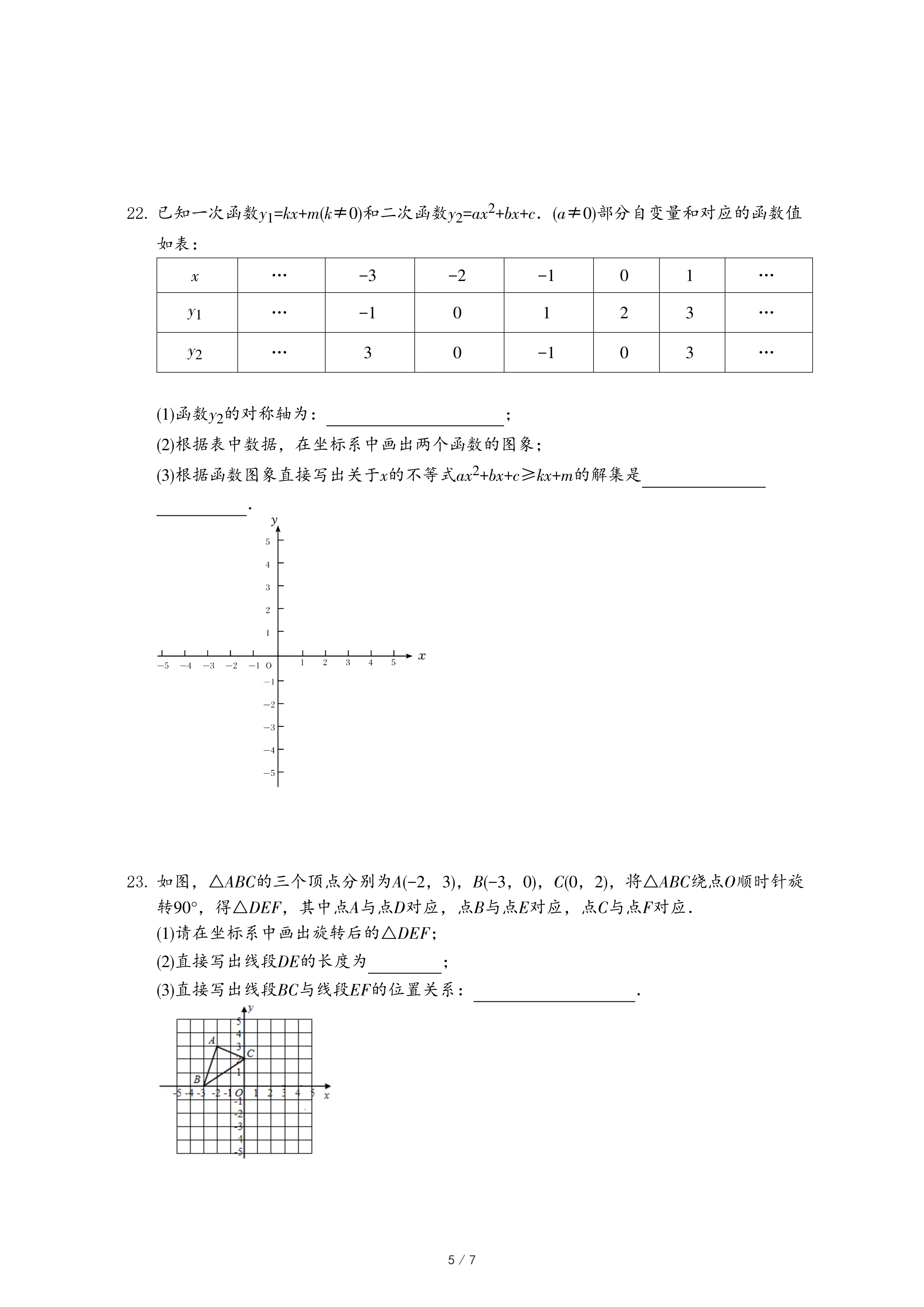
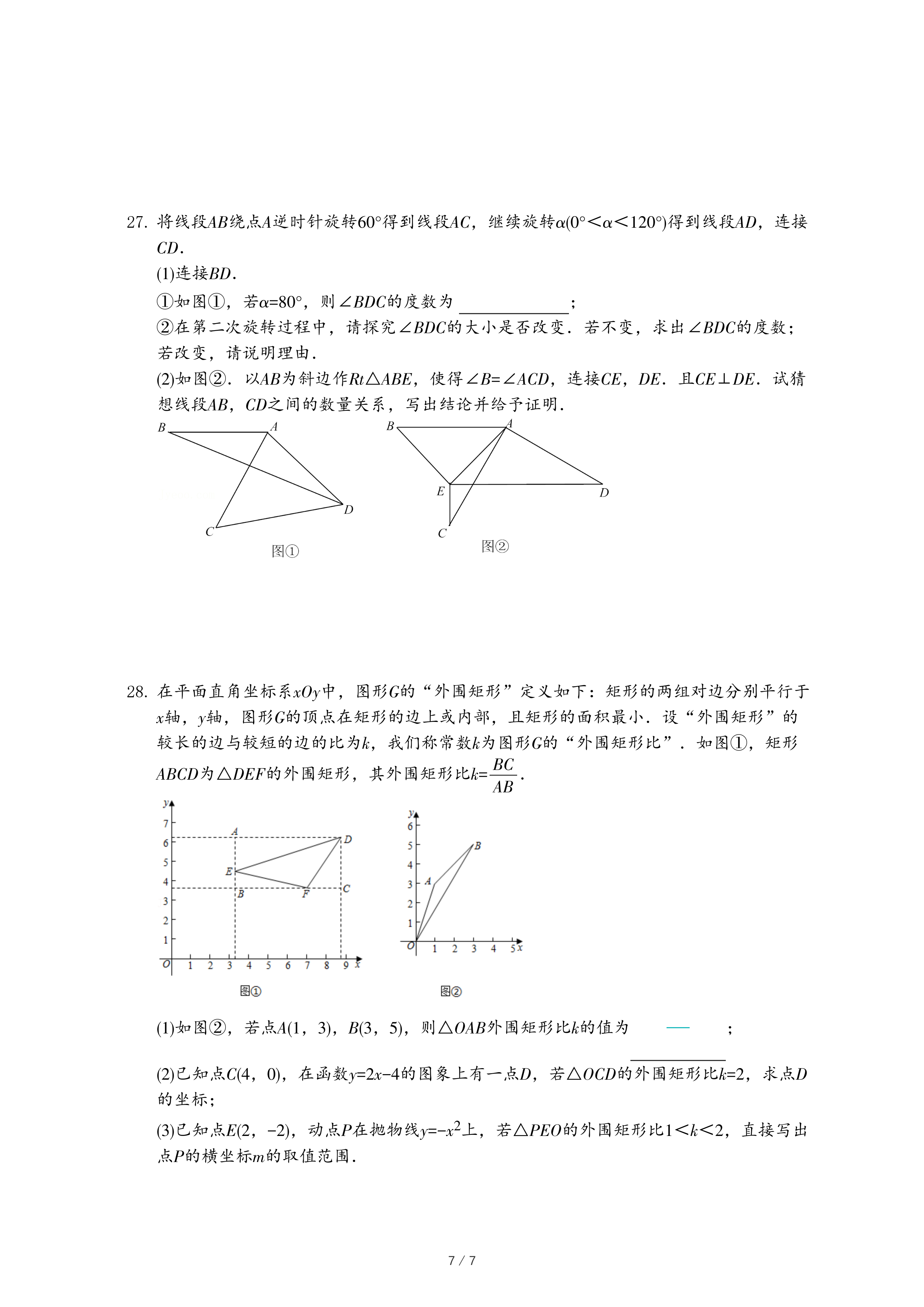
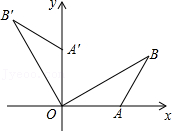
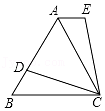
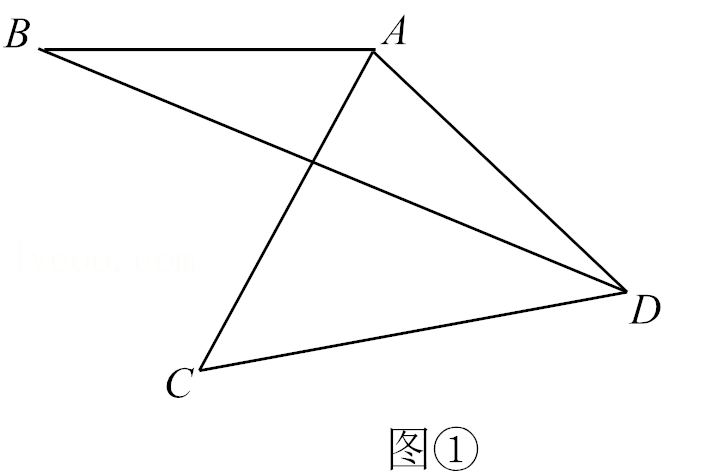
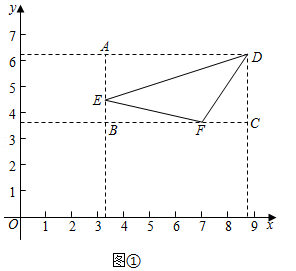
28.在平面直角坐标系xOy中,图形G的“外围矩形”定义如下:矩形的两组对边分别平行于x轴,y轴,图形G的顶点在矩形的边上或内部,且矩形的面积最小.设“外围矩形”的较长的边与较短的边的比为k,我们称常数k为图形G的“外围矩形比”.如图①,矩形ABCD为△DEF的外围矩形,其外围矩形比k=
.
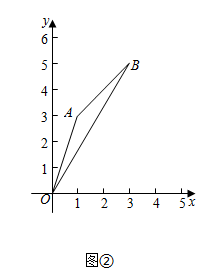
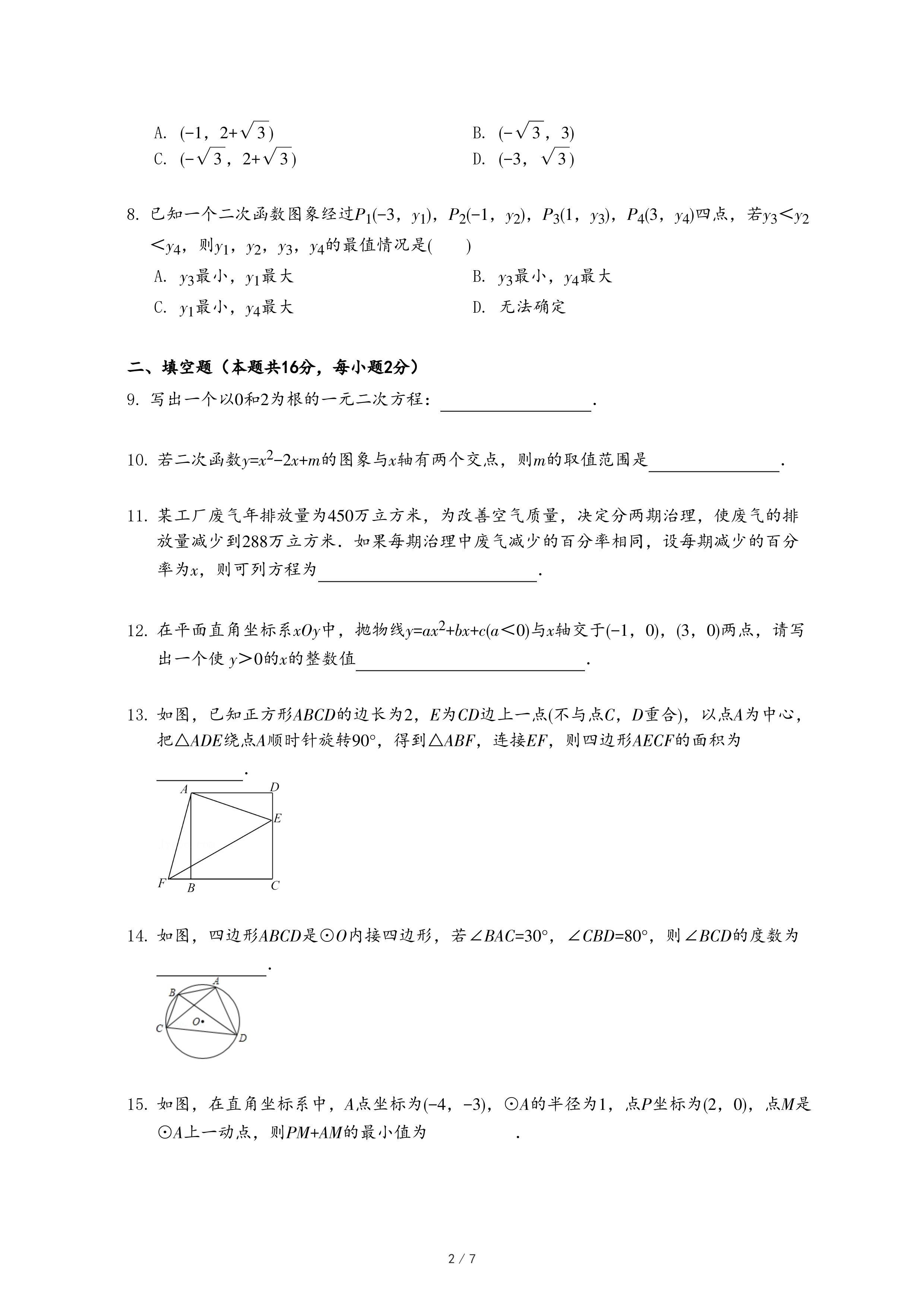
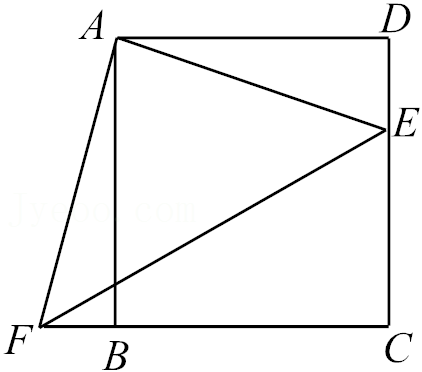
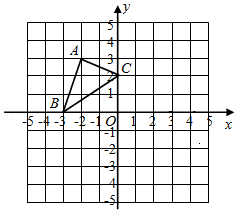
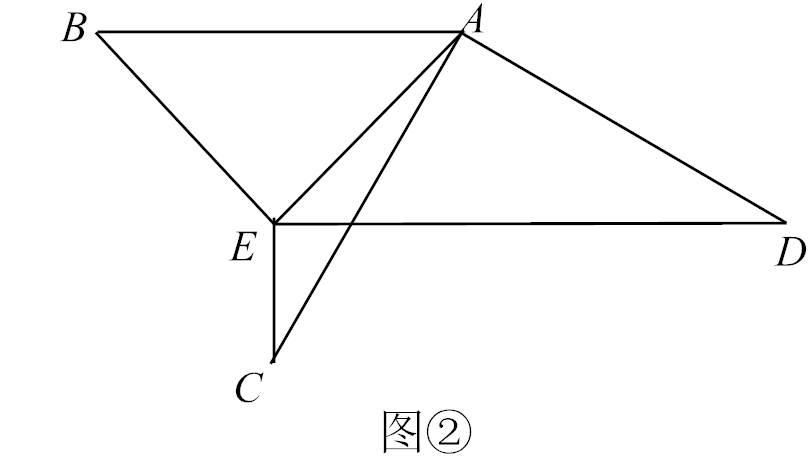
(1)如图②,若点A(1,3),B(3,5),则△OAB外围矩形比k的值为
;
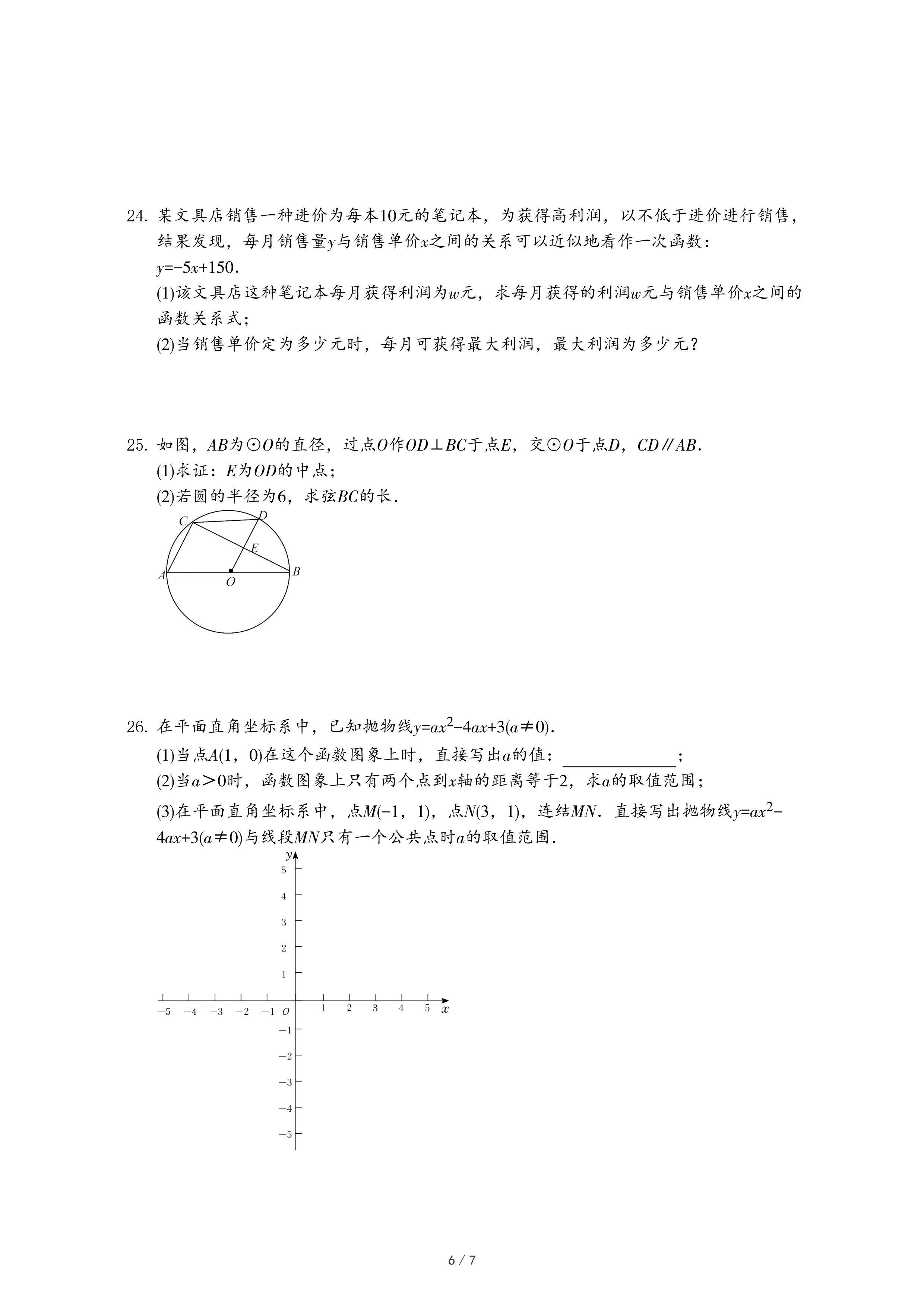
(2)已知点C(4,0),在函数y=2x-4的图象上有一点D,若△OCD的外围矩形比k=2,求点D的坐标;
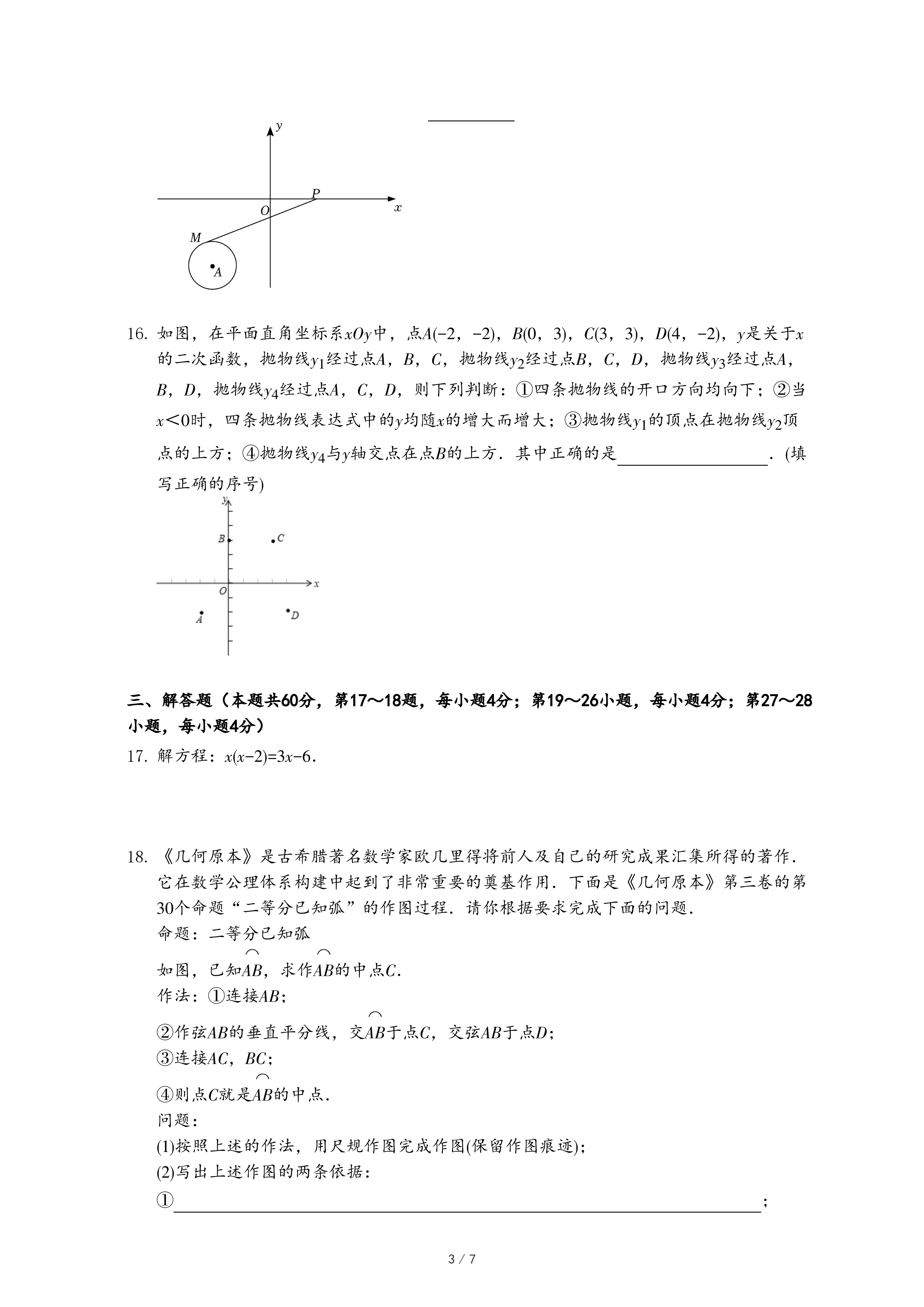
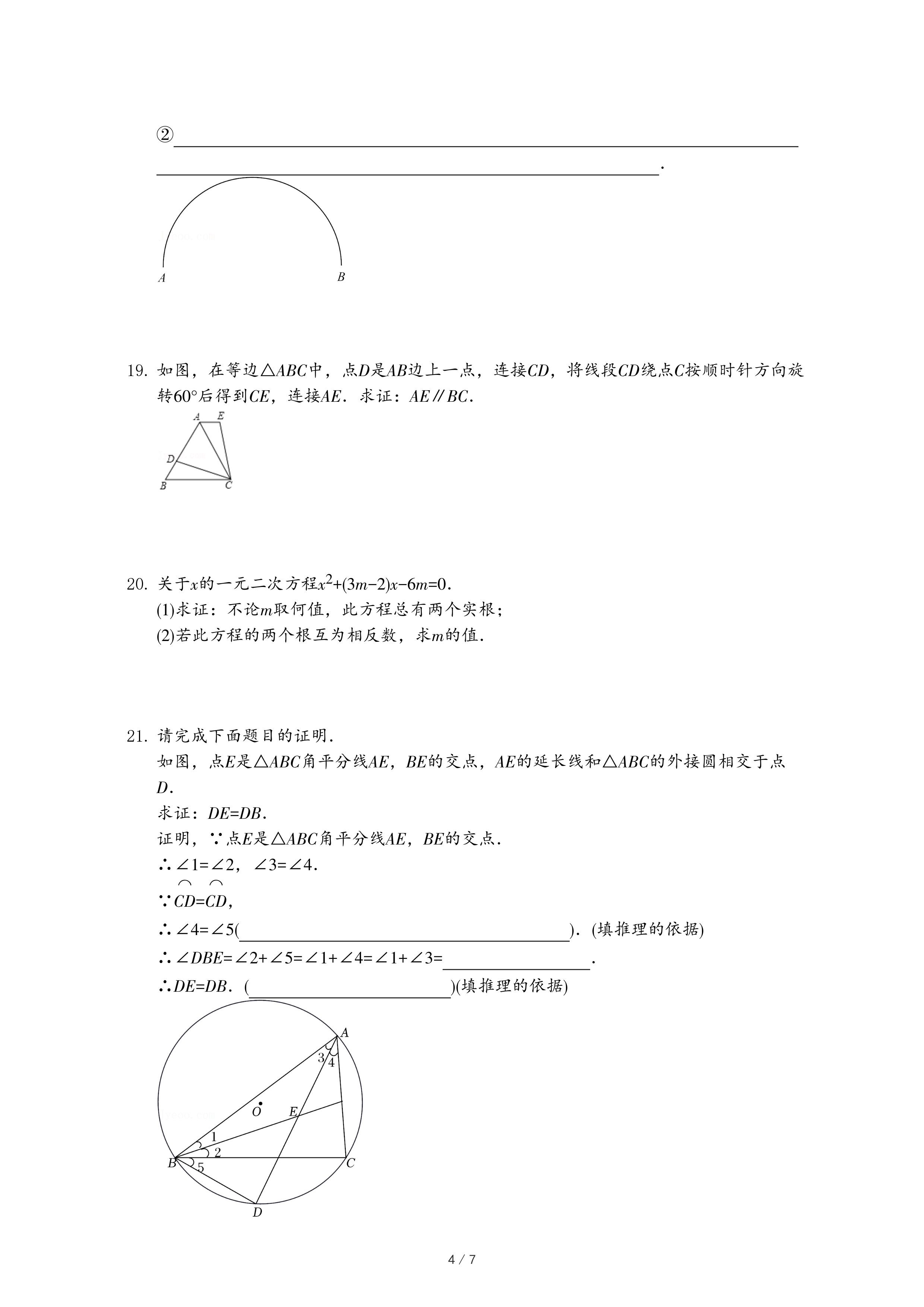
(3)已知点E(2,-2),动点P在抛物线y=-x
2上,若△PEO的外围矩形比1<k<2,直接写出点P的横坐标m的取值范围.