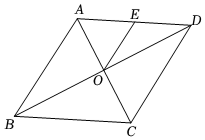
21.人口问题是“国之大者”,以习近平同志为核心的党中央高度重视人口问题,准确把握人口发展形势,有利于推动社会持续健康发展,为开启全面建设社会主义现代化国家新征程、向第二个百年奋斗目标进军创造良好的条件.某综合与实践研究小组根据我国第七次人口普查数据进行整理、描述和分析,给出部分数据信息:
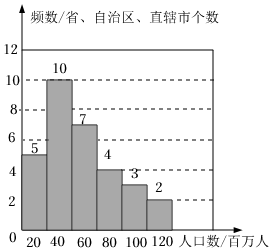
信息一:普查登记的全国大陆31个省、自治区、直辖市人口数的频数分布直方图如下:
(数据分成6组:0≤x<20,20≤x<40,40≤x<60,60≤x<80,80≤x<100,100≤x≤120)
信息二:普查登记的全国大陆31个省、自治区、直辖市人口数(百万人)在40≤x<60这一组的数据是:58,47,45,40,43,42,50;
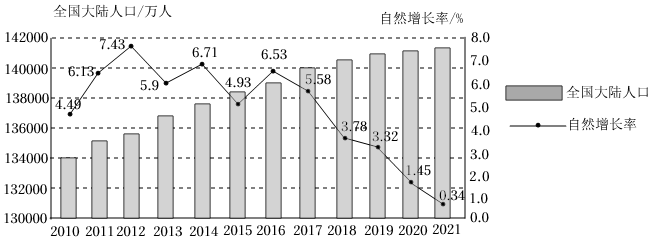
信息三:2010-2021年全国大陆人口数及自然增长率;
请根据以上信息,解答下列问题:
(1)普查登记的全国大陆31个省、自治区、直辖市人口数的中位数为
百万人.
(2)下列结论正确的是
.(只填序号)
①全国大陆31个省、自治区、直辖市中人口数大于等于100(百万人)的有2个地区;
②相对于2020年,2021年全国大陆人口自然增长率降低,全国大陆人口增长缓慢;
③2010-2021年全国大陆人口自然增长率持续降低.
(3)请写出2016-2021年全国大陆人口数、全国大陆人口自然增长率的变化趋势,结合变化趋势谈谈自己的看法.