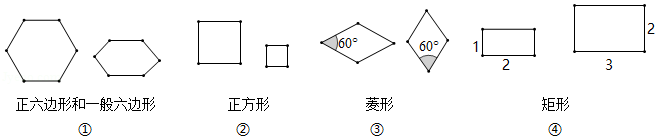
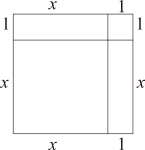
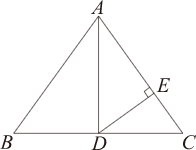
23.在习题课上,老师让同学们以课本一道习题“如图1,A、B、C、D四家工厂分别坐落在正方形城镇的四个角上.仓库E和Q分别位于AD和DC上,且ED=QC.证明两条直路BE=AQ且BE⊥AQ.”为背景开展数学探究.
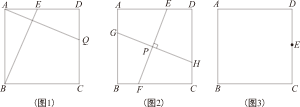
(1)独立思考:将上题条件中的ED=QC去掉,将结论中的BE⊥AQ变为条件,其他条件不变,那么BE=AQ还成立吗?请写出答案并说明理由;
(2)合作交流:“祖冲之”小组的同学受此问题的启发提出:如图2,在正方形ABCD内有一点P,过点P作EF⊥GH,点E、F分别在正方形的对边AD、BC上,点G、H分别在正方形的对边AB、CD上,那么EF与GH相等吗?并说明理由.
(3)拓展应用:“杨辉”小组的同学受“祖冲之”小组的启发,想到了利用图2的结论解决以下问题:
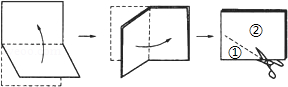
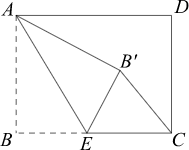
如图3,将边长为10
cm的正方形纸片ABCD折叠,使点A落在DC的中点E处,折痕为MN,点N在BC边上,点M在AD边上.请你画出折痕,则折痕MN的长是
;线段DM的长是
.