


| 1 |
| 2 |
| 1 |
| 2 |




| 5 |
| 8 |
| y+2a |
| y-1 |
| 3y-8 |
| 1-y |
| k |
| x |
| 11 |
| 8 |
| 7 |
| 3 |
| 21 |
| 4 |
| 21 |
| 2 |
| 4-x |
| 2 |
| 1 |
| 15 |
| a |
| a+2 |
| a2-4 |
| a2+4a+4 |
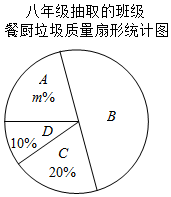
| 年级 | 平均数 | 中位数 | 众数 | 方差 | A等级所占百分比 |
| 七年级 | 1.3 | 1.1 | a | 0.26 | 40% |
| 八年级 | 1.3 | b | 1.0 | 0.23 | m% |
| 4-x2 |
| x2+1 |
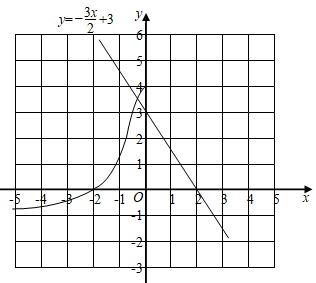
| x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … | ||||||||||
y=
| … | -
| -
| -
| 0 |
| 4 | 0 | ________ | ________ | ________ | … |
| 3 |
| 2 |
| 3 |
| 2 |
| 4-x2 |
| x2+1 |
| 29 |
| 25 |
| P(M) |
| Q(M) |
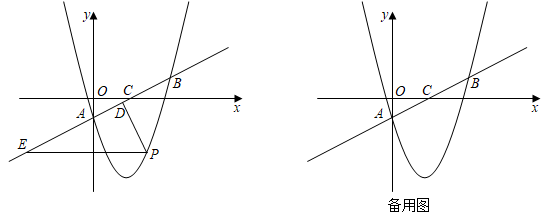
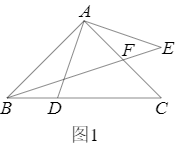
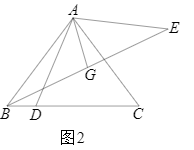
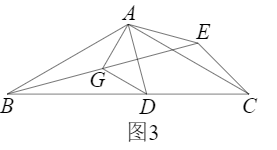
| BD-DG |
| CE |