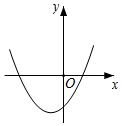
22.二次函数y=x
2-2mx的图象交x轴于原点O及点A.
感知特例
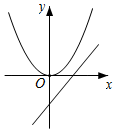
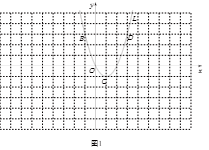
(1)当m=1时,如图1,抛物线L:y=x
2-2x上的点B,O,C,A,D分别关于点A中心对称的点为B′,O′,C′,A′,D′,如表:
| … | B(-1,3) | O(0,0) | C(1,-1) | A( ___,___) | D(3,3) | … |
| … | B'(5,-3) | O′(4,0) | C'(3,1) | A′(2,0) | D'(1,-3) | … |
①补全表格;
②在图1中描出表中对称后的点,再用平滑的曲线依次连接各点,得到的图象记为L'.
形成概念
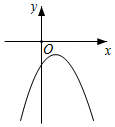
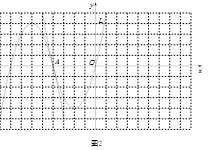
我们发现形如(1)中的图象L'上的点和抛物线L上的点关于点A中心对称,则称L'是L的“孔像抛物线”.例如,当m=-2时,图2中的抛物线L'是抛物线L的“孔像抛物线”.
探究问题
(2)①当m=-1时,若抛物线L与它的“孔像抛物线”L'的函数值都随着x的增大而减小,则x的取值范围为
;
②在同一平面直角坐标系中,当m取不同值时,通过画图发现存在一条抛物线与二次函数y=x
2-2mx的所有“孔像抛物线”L'都有唯一交点,这条抛物线的解析式可能是
(填“y=ax
2+bx+c”或“y=ax
2+bx”或“y=ax
2+c”或“y=ax
2”,其中abc≠0);
③若二次函数y=x
2-2mx及它的“孔像抛物线”与直线y=m有且只有三个交点,求m的值.