24.点A是半径为2
√3
的⊙O上一动点,点B是⊙O外一定点,OB=6.连接OA、AB.
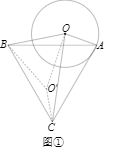
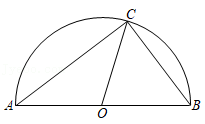
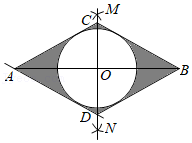
(1)【阅读感知】如图①,当△ABC是等边三角形时,连接OC,求OC的最大值;
将下列解答过程补充完整.
解:将线段OB绕点B顺时针旋转60°到O′B,连接OO′、CO′.
由旋转的性质知:∠OBO′=60°,BO′=BO=6,即△OBO′是等边三角形.
∴OO′=BO=6
又∵△ABC是等边三角形
∴∠ABC=60°,AB=BC
∴∠OBO′=∠ABC=60°
∴∠OBA=∠O′BC
在△OBA和△O′BC中,
∴
(
SAS)
∴OA=O′C
在△OO′C中,OC<OO′+O′C
当O、O′、C三点共线,且点C在OO′的延长线上时,OC=OO′+O′C
即OC≤OO′+O′C
∴当O、O′、C三点共线,且点C在OO′的延长线上时,OC取最大值,最大值是
.
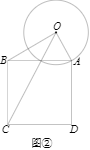
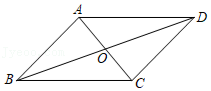
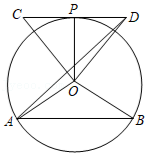
(2)【类比探究】如图②,当四边形ABCD是正方形时,连接OC,求OC的最小值;
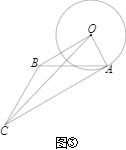
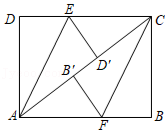
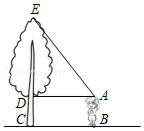
(3)【理解运用】如图③,当△ABC是以AB为腰,顶角为120°的等腰三角形时,连接OC,求OC的最小值,并直接写出此时△ABC的周长.