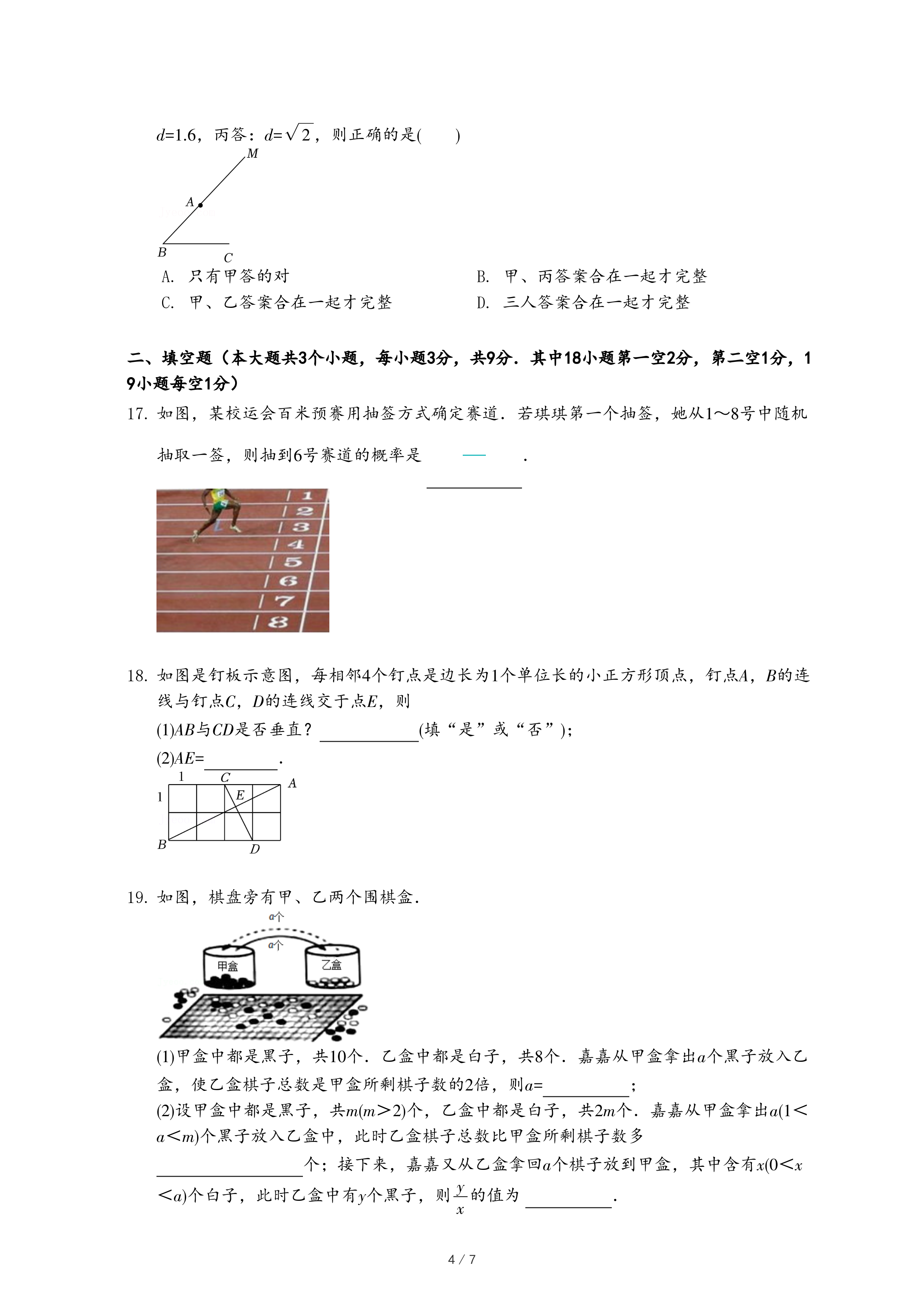
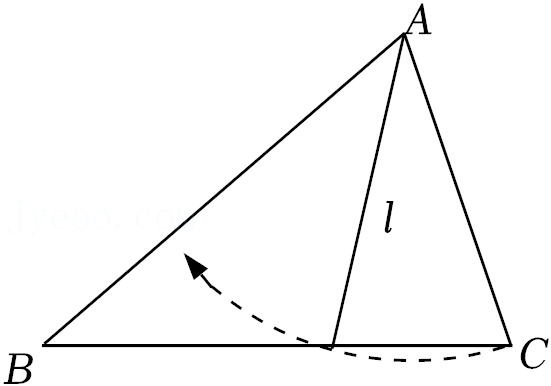
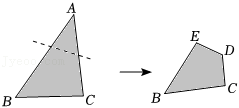
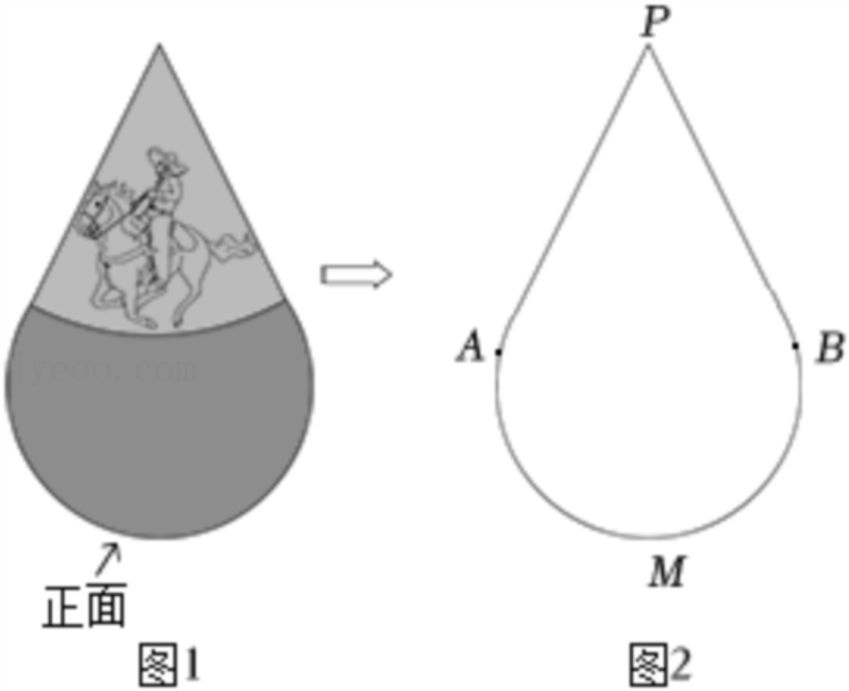
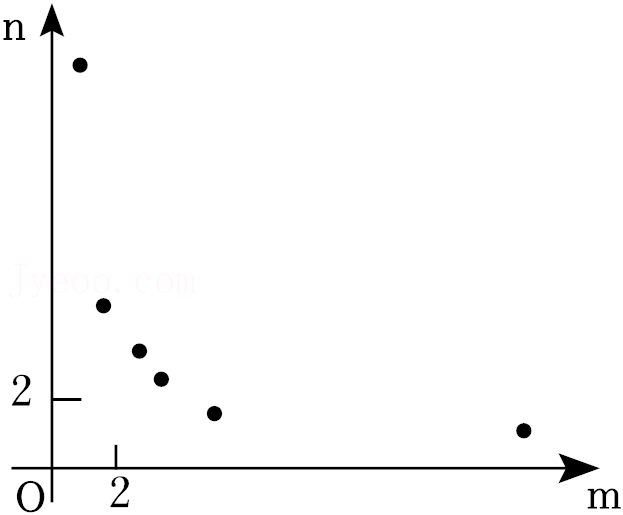
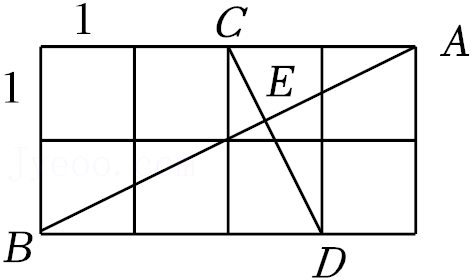
26.如图1,四边形ABCD中,AD∥BC,∠ABC=90°,∠C=30°,AD=3,AB=2
√3
,DH⊥BC于点H.将△PQM与该四边形按如图方式放在同一平面内,使点P与A重合,点B在PM上,其中∠Q=90°,∠QPM=30°,PM=4
√3
.
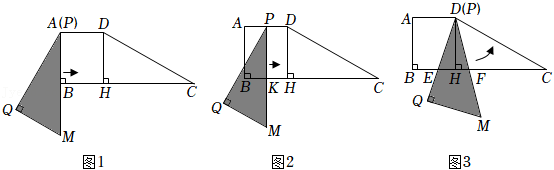
(1)求证:△PQM≌△CHD;
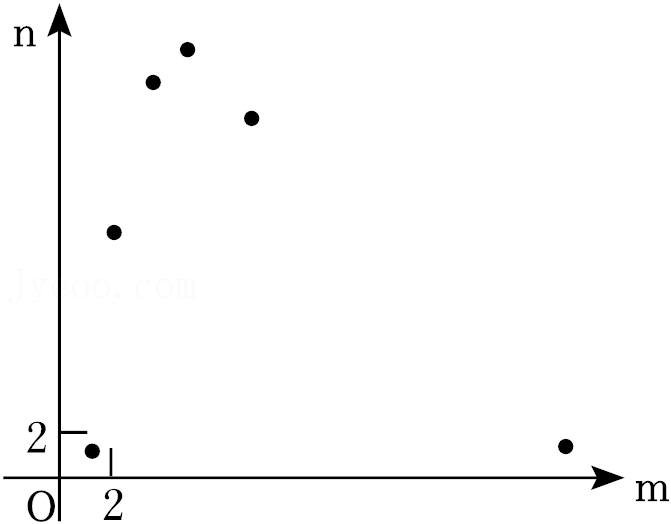
(2)△PQM从图1的位置出发,先沿着BC方向向右平移(图2),当点P到达点D后立刻绕点D逆时针旋转(图3),当边PM旋转50°时停止.
①边PQ从平移开始,到绕点D旋转结束,求边PQ扫过的面积;
②如图2,点K在BH上,且BK=9-4
√3
.若△PQM右移的速度为每秒1个单位长,绕点D旋转的速度为每秒5°,求点K在△PQM区域(含边界)内的时长;
③如图3,在△PQM旋转过程中,设PQ,PM分别交BC于点E,F,若BE=d,直接写出CF的长(用含d的式子表示).