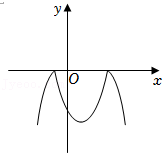
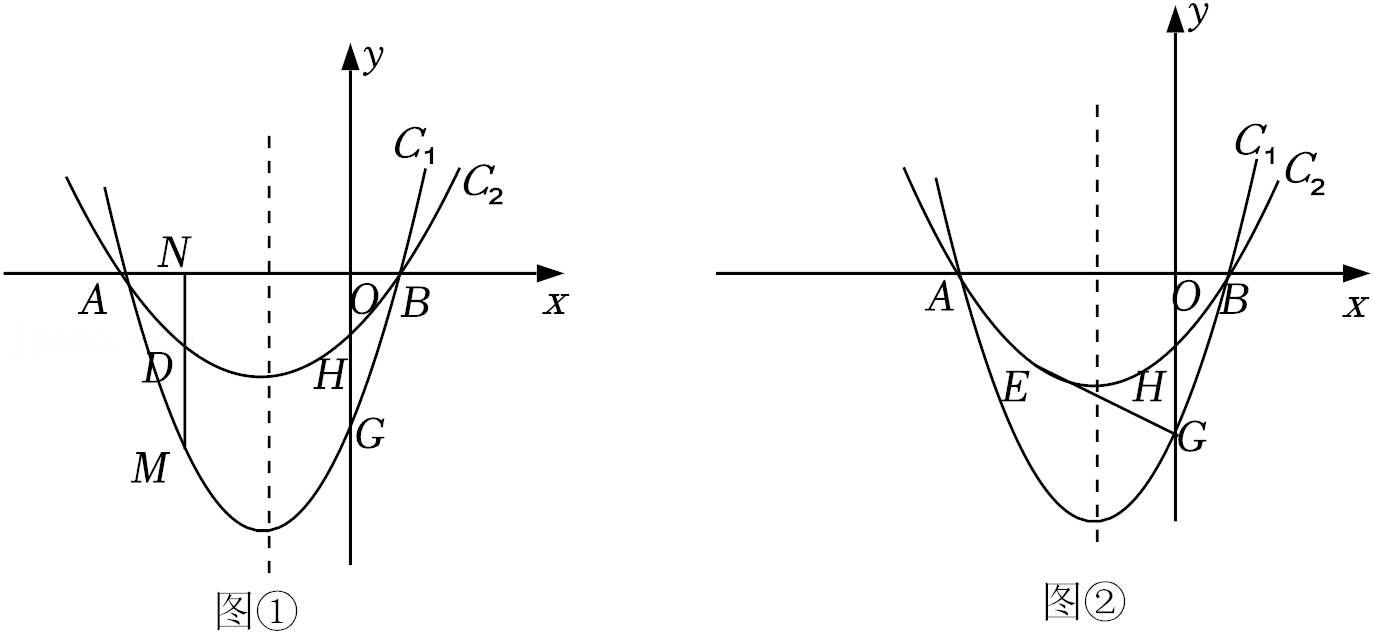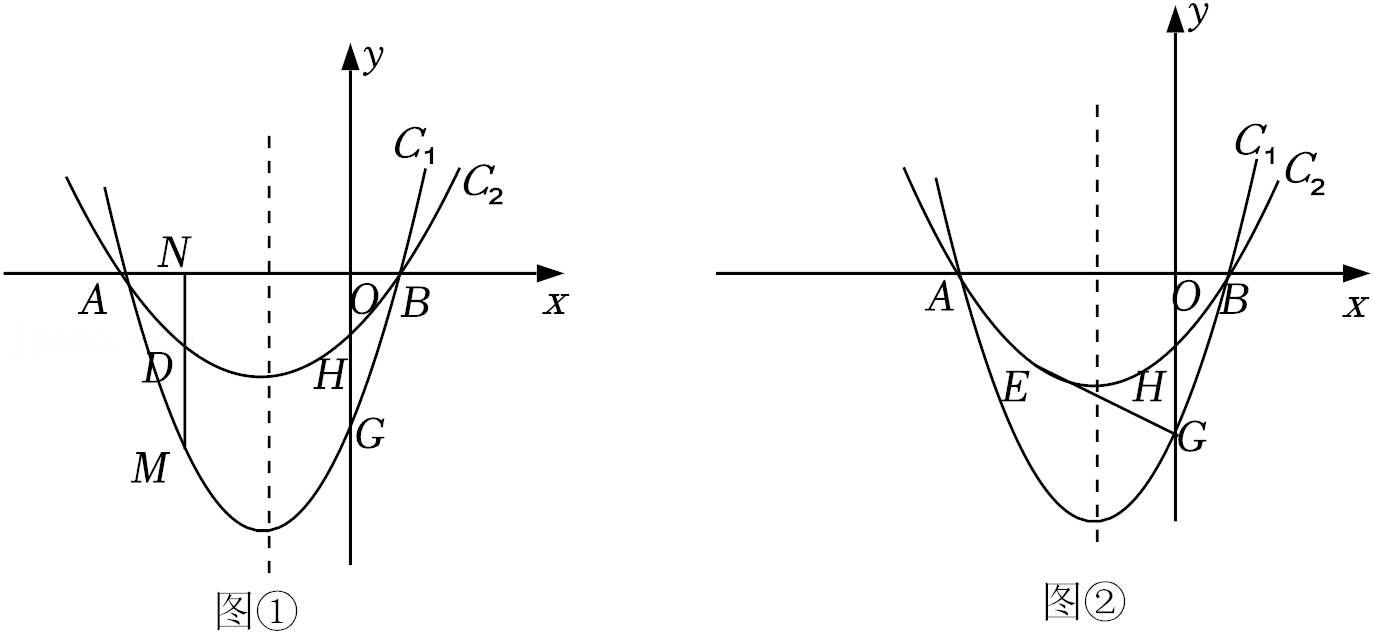26.定义:由两条与x轴有着相同的交点,并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”,如图①,抛物线C
1:y=x
2+2x-3与抛物线C
2:y=ax
2+2ax+c组成一个开口向上的“月牙线”,抛物线C
1和抛物线C
2与x轴有着相同的交点A(-3,0)、B(点B在点A右侧),与y轴的交点分别为G、H(0,-1).
(1)求抛物线C
2的解析式和点G的坐标.
(2)点M是x轴下方抛物线C
1上的点,过点M作MN⊥x轴于点N,交抛物线C
2于点D,求线段MN与线段DM的长度的比值.
(3)如图②,点E是点H关于抛物线对称轴的对称点,连接EG,在x轴上是否存在点F,使得△EFG是以EG为腰的等腰三角形?若存在,请求出点F的坐标;若不存在,请说明理由.