


| 1 |
| 37 |
| 1 |
| 37 |
| { | x+y−4=0, 2x−y+m=0 |
| { | x=−1, y=5 |
| { | x=1, y=3 |
| { | x=3, y=1 |
| { | x=9, y=−5 |

| 1 |
| 2 |
| 1 |
| 7 |
| { | x+2>−1 x−5≤3(x−1) |
| a+1 |
| a-1 |
| 2a |
| a2-1 |
| 输入x | … | -6 | -4 | -2 | 0 | 2 | … |
| 输出y | … | -6 | -2 | 2 | 6 | 16 | … |

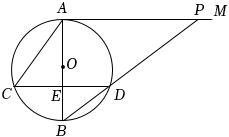
| 组别 | “劳动时间”t/分钟 | 频数 | 组内学生的平均“劳动时间”/分钟 |
| A | t<60 | 8 | 50 |
| B | 60≤t<90 | 16 | 75 |
| C | 90≤t<120 | 40 | 105 |
| D | t≥120 | 36 | 150 |