25.小云统计了自己所住小区5月1日至30日的厨余垃圾分出量(单位:千克),相关信息如下:
a.小云所住小区5月1日至30日的厨余垃圾分出量统计图:
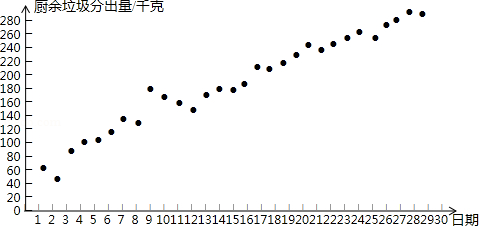
b.小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下:
| 时段 | 1日至10日 | 11日至20日 | 21日至30日 |
| 平均数 | 100 | 170 | 250 |
(1)该小区5月1日至30日的厨余垃圾分出量的平均数约为
(结果取整数);
(2)已知该小区4月的厨余垃圾分出量的平均数为60,则该小区5月1日至30日的厨余垃圾分出量的平均数约为4月的
倍(结果保留小数点后一位);
(3)记该小区5月1日至10日的厨余垃圾分出量的方差为s
12,5月11日至20日的厨余垃圾分出量的方差为s
22,5月21日至30日的厨余垃圾分出量的方差为s
32.直接写出s
12,s
22,s
32的大小关系.