27.【概念认识】城市的许多街道是相互垂直或平行的,因此,往往不能沿直线行走到达目的地,只能按直角拐弯的方式行走.可以按照街道的垂直和平行方向建立平面直角坐标系xOy,对两点A(x
1,y
1)和B(x
2,y
2),用以下方式定义两点间距离:d(A,B)=|x
1-x
2|+|y
1-y
2|.
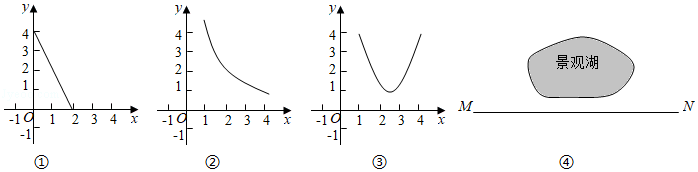
【数学理解】(1)①已知点A(-2,1),则d(O,A)=
.
②函数y=-2x+4(0≤x≤2)的图象如图①所示,B是图象上一点,d(O,B)=3,则点B的坐标是
.
(2)函数y=
(x>0)的图象如图②所示.求证:该函数的图象上不存在点C,使d(O,C)=3.
(3)函数y=x
2-5x+7(x≥0)的图象如图③所示,D是图象上一点,求d(O,D)的最小值及对应的点D的坐标.
【问题解决】(4)某市要修建一条通往景观湖的道路,如图④,道路以M为起点,先沿MN方向到某处,再在该处拐一次直角弯沿直线到湖边,如何修建能使道路最短?(要求:建立适当的平面直角坐标系,画出示意图并简要说明理由)