



| 1 |
| 100 |
| 1 |
| 100 |
| 1 |
| x+1 |
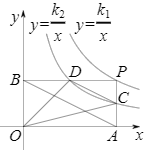
| k1 |
| x |
| k2 |
| x |
| k1-k2 |
| 2 |
| (k1-k2)2 |
| 2k1 |
| 1 |
| 3 |
| 1 |
| a |
| 1 |
| b |
| { | 2x+y=7 x=y-1 |

| 喜欢程度 | 人数 |
| A.非常喜欢 | 50人 |
| B.比较喜欢 | m人 |
| C.无所谓 | n人 |
| D.不喜欢 | 16人 |
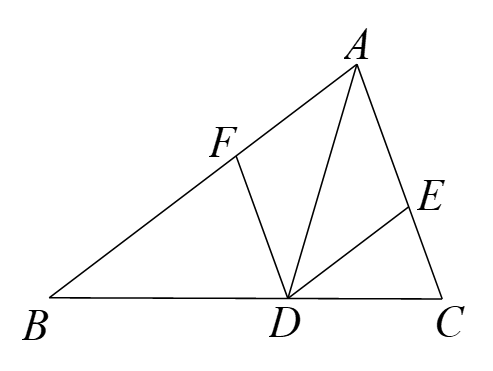
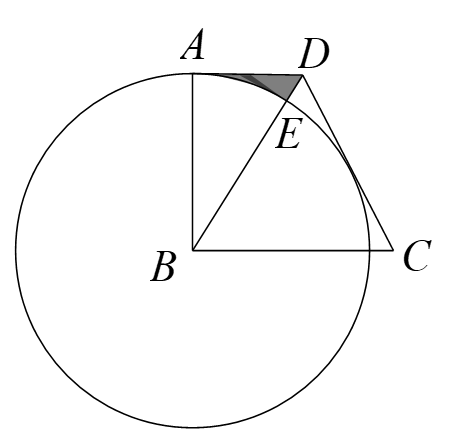
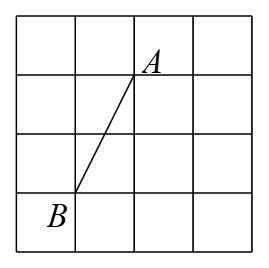
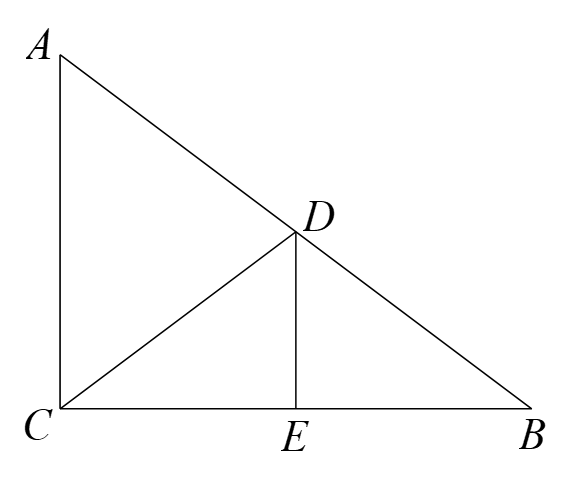
| 已知线段BC=2,使用作图工具作∠BAC=30°,尝试操作后思考:(1)这样的点A唯一吗?(2)点A的位置有什么特征?你有什么感悟? |
| 4 |
| 3 |
| 2 |
| 3 |
| 甲公司经理:如果我公司每辆汽车月租费3000元,那么50辆汽车可以全部租出.如果每辆汽车的月租费每增加50元,那么将少租出1辆汽车.另外,公司为每辆租出的汽车支付月维护费200元.乙公司经理:我公司每辆汽车月租费3500元,无论是否租出汽车,公司均需一次性支付月维护费共计1850元. |